【题目】已知a,b,c是![]() ABC中角A,B,C的对边,S是
ABC中角A,B,C的对边,S是![]() ABC的面积.若a2+c2=b2+ac,
ABC的面积.若a2+c2=b2+ac,
(I)求角B ; (II)若b=2,S=![]() ,判断三角形形状
,判断三角形形状
参考答案:
【答案】(I)![]() ;(Ⅱ)等边三角.
;(Ⅱ)等边三角.
【解析】试题分析:
(1)利用题意首先求得![]() 的值,然后利用特殊角的三角函数值求解
的值,然后利用特殊角的三角函数值求解![]() 的大小即可;
的大小即可;
(2)利用三角形的面积公式确定![]() 即可确定△ABC为等边三角形.
即可确定△ABC为等边三角形.
试题解析:
(I)由![]() 得
得![]()
又因为![]()
所以![]()
又![]() 所以
所以![]()
(Ⅱ)![]() ,得
,得![]()
又![]() ,所以
,所以 ![]() ,得
,得![]()
故三角形为等边三角
点睛:在解三角形的问题中,三角形内角和定理起着重要作用,在解题时要注意根据这个定理确定角的范围及三角函数值的符号,防止出现增解或漏解.
正、余弦定理在应用时,应注意灵活性,尤其是其变形应用时可相互转化.如a2=b2+c2-2bccos A可以转化为sin2 A=sin2 B+sin2 C-2sin Bsin Ccos A,利用这些变形可进行等式的化简与证明.
判断三角形形状的两种途径,一是化边为角;二是化角为边,并常用正弦(余弦)定理实施边、角转换.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 空间不同的三点确定一个平面
B. 空间两两相交的三条直线确定一个平面
C. 空间有三个角为直角的四边形一定是平面图形
D. 和同一条直线相交的三条平行直线一定在同一平面内
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 ,
,(1)若曲线
 在点
在点 处的切线为
处的切线为 ,求
,求 的值;
的值;(2)讨论函数
 的单调性;
的单调性;(3)设函数
 ,若至少存在一个
,若至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范.
的取值范. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表提供了某公司技术升级后生产
 产品过程中记录的产量
产品过程中记录的产量 (吨)与相应的成本
(吨)与相应的成本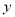 (万元)的几组对照数据:
(万元)的几组对照数据:
(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出
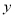 对
对 的回归直线方程;
的回归直线方程;(3)已知该公司技术升级前生产100吨
 产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨
产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨 产品的成本比技术升级前约降低多少万元?
产品的成本比技术升级前约降低多少万元?(附:
 ,
,  ,其中
,其中 为样本平均值)
为样本平均值) -
科目: 来源: 题型:
查看答案和解析>>【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用
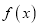 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(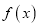 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),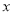 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 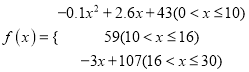 .
.(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
-
科目: 来源: 题型:
查看答案和解析>>【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修,可供利用的旧墙足够长),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图2所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m, 设利用旧墙的长度为
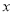 (单位:
(单位: 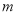 ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为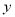 (单位:元).
(单位:元).
(Ⅰ)将
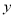 表示为
表示为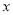 的函数;
的函数;(Ⅱ)试确定
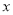 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,且曲线
,且曲线 的左焦点
的左焦点 在直线
在直线 上.
上.(1)若直线
 与曲线
与曲线 交于
交于 两点,求
两点,求 的值;
的值;(2)求曲线
 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
相关试题

