【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 与坐标轴的交点都在圆
与坐标轴的交点都在圆![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)若圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
分析:(1)因为曲线![]() 与坐标轴的交点都在圆
与坐标轴的交点都在圆![]() 上,所以要求圆的方程应求曲线与坐标轴的三个交点。曲线
上,所以要求圆的方程应求曲线与坐标轴的三个交点。曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]()
![]() .由与
.由与![]() 轴的交点为
轴的交点为![]()
![]() 关于点(3,0)对称,故可设圆
关于点(3,0)对称,故可设圆![]() 的圆心为
的圆心为![]() ,由两点间距离公式可得
,由两点间距离公式可得![]() ,解得
,解得![]() .进而可求得圆
.进而可求得圆![]() 的半径为
的半径为![]() ,然后可求圆
,然后可求圆![]() 的方程为
的方程为![]() .(2)设
.(2)设![]() ,
,![]() ,由
,由![]() 可得
可得![]() ,进而可得
,进而可得![]() ,减少变量个数。因为
,减少变量个数。因为![]() ,
,![]() ,所以
,所以![]() .要求值,故将直线与圆的方程联立可得
.要求值,故将直线与圆的方程联立可得![]() ,消去
,消去![]() ,得方程
,得方程![]() 。因为直线与圆有两个交点,故判别式
。因为直线与圆有两个交点,故判别式![]() ,由根与系数的关系可得
,由根与系数的关系可得![]() ,
,![]() .代入
.代入![]() ,化简可求得
,化简可求得![]() ,满足
,满足![]() ,故
,故![]() .
.
详解:(1)曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为
![]()
![]() .故可设
.故可设![]() 的圆心为
的圆心为![]() ,则有
,则有![]() ,解得
,解得![]() .则圆
.则圆![]() 的半径为
的半径为![]() ,所以圆
,所以圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,其坐标满足方程组
,其坐标满足方程组![]()
消去![]() ,得方程
,得方程![]() .
.
由已知可得,判别式![]() ,且
,且![]() ,
,![]() .
.
由于![]() ,可得
,可得![]() .
.
又![]() ,
,![]()
所以![]() .
.
由得![]() ,满足
,满足![]() ,故
,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的公差d≠0,它的前n项和为Sn,若S5=70,且a2,a7,a22成等比数列.
(1)求数列{an}的通项公式;
(2)设数列
 的前n项和为Tn,求证:
的前n项和为Tn,求证: 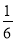 ≤Tn<
≤Tn<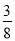 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若
 =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}前n项和为Sn,已知
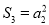 ,且S1,S2,S4成等比数列,求{an}的通项公式.
,且S1,S2,S4成等比数列,求{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明
 是等比数列,并求{an}的通项公式;
是等比数列,并求{an}的通项公式;(2)证明:
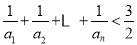 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 、
、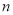 是两条不同的直线,
是两条不同的直线, 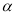 ,
, 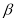 ,
,  是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:①若
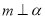 ,
, 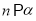 ,则
,则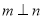 ②若
②若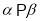 ,
, 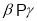 ,
, 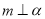 ,则
,则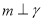
③若
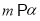 ,
, 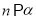 ,则
,则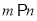 ④若
④若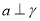 ,
, 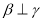 ,则
,则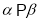
其中正确命题的序号是( ).
A. ①和② B. ②和③ C. ③和④ D. ①和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,平面
,平面 底面
底面 ,
, .
. 和
和 分别是
分别是 和
和 的中点,求证:
的中点,求证:
(Ⅰ)
 底面
底面 ;
;(Ⅱ)
 平面
平面 ;
;(Ⅲ)平面
 平面
平面 .
.
相关试题

