【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明![]() 是等比数列,并求{an}的通项公式;
是等比数列,并求{an}的通项公式;
(2)证明: ![]() .
.
参考答案:
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:
(1)结合题中所给的递推关系可得: 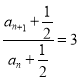 ,据此可得数列
,据此可得数列![]() 是首项为
是首项为![]() ,公比为3的等比数列;
,公比为3的等比数列;
(2)结合(1)的结论可得![]() ,据此进行放缩后求和即可证得题中的结论.
,据此进行放缩后求和即可证得题中的结论.
试题解析:
(1)由an+1=3an+1得an+1+![]() =3
=3![]() ,所以
,所以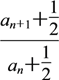 =3,
=3,
所以![]() 是等比数列,首项为a1+
是等比数列,首项为a1+![]() =
=![]() ,公比为3,
,公比为3,
所以an+![]() =
=![]() ·3n-1,
·3n-1,
因此{an}的通项公式为an=![]() (n∈N*).
(n∈N*).
(2)由(1)知:an=![]() ,所以
,所以![]() =
=![]() ,
,
因为当n≥1时,3n-1≥2·3n-1,
所以![]() ≤
≤![]() ,
,
于是![]() +
+![]() +…+
+…+![]() ≤1+
≤1+![]() +…+
+…+![]() =
=![]()
![]() <
<![]() ,
,
所以![]() +
+![]() +…+
+…+![]() <
<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若
 =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}前n项和为Sn,已知
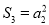 ,且S1,S2,S4成等比数列,求{an}的通项公式.
,且S1,S2,S4成等比数列,求{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.(1)求圆
 的方程;
的方程;(2)若圆
 与直线
与直线 交于
交于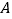 ,
, 两点,且
两点,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 、
、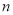 是两条不同的直线,
是两条不同的直线, 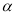 ,
, 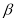 ,
,  是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:①若
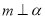 ,
, 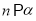 ,则
,则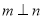 ②若
②若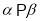 ,
, 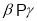 ,
, 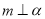 ,则
,则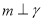
③若
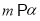 ,
, 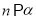 ,则
,则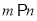 ④若
④若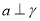 ,
, 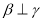 ,则
,则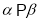
其中正确命题的序号是( ).
A. ①和② B. ②和③ C. ③和④ D. ①和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,平面
,平面 底面
底面 ,
, .
. 和
和 分别是
分别是 和
和 的中点,求证:
的中点,求证:
(Ⅰ)
 底面
底面 ;
;(Ⅱ)
 平面
平面 ;
;(Ⅲ)平面
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
 中,
中, ,
, 点在直线
点在直线 上,若
上,若 的面积为10,求
的面积为10,求 点的坐标.
点的坐标.
相关试题

