【题目】已知函数![]() ,
, ![]() (其中
(其中![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 有两个不同零点,求实数
有两个不同零点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .(2)
.(2)![]()
【解析】试题分析:(1)先根据导数几何意义得切线斜率![]() ,解出
,解出![]() ,再求导函数零点,根据导函数符号确定函数单调区间,(2)先化简
,再求导函数零点,根据导函数符号确定函数单调区间,(2)先化简![]() ,再求导数,利用参变分离转化为研究两曲线交点个数问题:函数
,再求导数,利用参变分离转化为研究两曲线交点个数问题:函数![]() 的图象与函数
的图象与函数![]() 的图像有两个不同交点,再利用导数研究函数
的图像有两个不同交点,再利用导数研究函数![]() 图像,结合图像确定有两个交点需满足的条件
图像,结合图像确定有两个交点需满足的条件
试题解析:解:(Ⅰ)因为![]()
所以![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
由于曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,
轴平行,
所以![]() ,因此
,因此![]() ;
;
所以![]()
令![]() ,
, ![]() ,
, ![]()
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
又因为![]() ,
,
所以当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
因此![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(Ⅱ)由(Ⅰ)知, ![]()
又因为![]() ,
, ![]() ,
,
所以![]() ,
,
由![]() 得
得![]() ,令
,令![]() ,
,
所以函数![]() 有两个不同零点等价于函数
有两个不同零点等价于函数![]() 的图象与函数
的图象与函数![]() 的图像有两个不同交点,
的图像有两个不同交点,
又因为![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时, img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/17/cc31a5e0/SYS201712291718517226540281_DA/SYS201712291718517226540281_DA.052.png" width="64" height="27" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
时, img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/17/cc31a5e0/SYS201712291718517226540281_DA/SYS201712291718517226540281_DA.052.png" width="64" height="27" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增,
上单调递增,
因此![]() ,
,
又因为![]() ,
, ![]() ,
,
所以![]() ,则
,则![]() ,
,
结合函数图像可得,当![]() 时,函数
时,函数![]() 的图像与函数
的图像与函数![]() 的图像有两个不同交点,
的图像有两个不同交点,
即当![]() 时, 函数
时, 函数![]() 有两个不同零点,
有两个不同零点,
综上可得,所求实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系: f(t)=10﹣
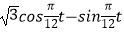 ,t∈[0,24)
,t∈[0,24)
(Ⅰ)求实验室这一天的最大温差;
(Ⅱ)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的值满足f(x)<0,对任意实数x,y都有f(xy)=f(x)f(y),且f(﹣1)=1,f(27)=9,当0<x<1时,f(x)∈(0,1).
(1)求f(1)的值,判断f(x)的奇偶性并证明;
(2)判断f(x)在(0,+∞)上的单调性,并给出证明;
(3)若a≥0且f(a+1)≤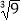 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)的定义域为[0,4],则函数g(x)=f(x)+f(x2)的定义域为( )
A.[0,2]
B.[0,16]
C.[﹣2,2]
D.[﹣2,0] -
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
A1
A2
A3
A4
A5
质量指标
(x , y , z)(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标
(x , y , z)(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用上表提供的样本数据估计该批产品的一等品率.
(2)在该样品的一等品中,随机抽取2件产品, ①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 中,
中,  分别为两腰上的高、求证:
分别为两腰上的高、求证: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
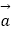 =(cosα,sinα),
=(cosα,sinα), 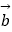 =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若|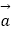 ﹣
﹣ 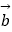 |=
|= 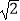 ,求证:
,求证: 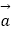 ⊥
⊥ 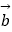 ;
;
(2)设c=(0,1),若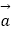 +
+ 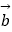 =c,求α,β的值.
=c,求α,β的值.
相关试题

