【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,
, ![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)曲线C的参数方程为![]() (α为参数),利用平方关系可得曲线C的普通方程.由直线l的极坐标方程为
(α为参数),利用平方关系可得曲线C的普通方程.由直线l的极坐标方程为![]() ,展开化为:ρsinθ+ρcosθ=2,利用互化公式可得:直线l的普通方程,利用斜率与倾斜角的关系即可得出.
,展开化为:ρsinθ+ρcosθ=2,利用互化公式可得:直线l的普通方程,利用斜率与倾斜角的关系即可得出.
(2)显然点![]() 在直线l
在直线l![]() 上.在平面直角坐标系xOy中,直线l的参数方程是
上.在平面直角坐标系xOy中,直线l的参数方程是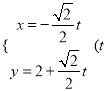 为参数).将直线l的参数方程代入曲线C的普通方程,得到关于t的一元二次方程,此方程的两根为直线l与曲线C的交点A,B对应的参数tA,tB,利用|PA|+|PB|=|tA|+|tB|即可得出.
为参数).将直线l的参数方程代入曲线C的普通方程,得到关于t的一元二次方程,此方程的两根为直线l与曲线C的交点A,B对应的参数tA,tB,利用|PA|+|PB|=|tA|+|tB|即可得出.
试题解析:
(Ⅰ)由![]() 消去参数α,得
消去参数α,得![]() ,
,
即C的普通方程为![]() .
.
由![]() ,得ρsinθ+ρcosθ=2,…(*)
,得ρsinθ+ρcosθ=2,…(*)
将![]() 代入(*),化简得
代入(*),化简得![]() ,
,
所以直线l的倾斜角为![]() .
.
(Ⅱ)由(Ⅰ)知,点P(0,2)在直线l上,可设直线l的参数方程为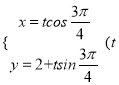 为参数),即
为参数),即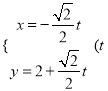 为参数),代入
为参数),代入![]() 并化简,得
并化简,得![]() .
.
![]() .
.
设A,B两点对应的参数分别为t1,t2,
则![]() ,所以t1<0,t2<0,
,所以t1<0,t2<0,
所以![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】班主任为了对本班学生的考试成绩进行分析,决定从全班
 位女同学,
位女同学,  位男同学中随机
位男同学中随机抽取一个容量为
 的样本进行分析.
的样本进行分析.(Ⅰ)如果按性别比例分层抽样,求样本中男生、女生人数分别是多少;
(Ⅱ)随机抽取
 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为:  ;物理成绩由低到高依次为:
;物理成绩由低到高依次为:  ,若规定
,若规定 分(含
分(含 分)以上为优秀,记
分)以上为优秀,记 为这
为这 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
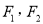 是椭圆
是椭圆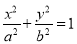 的左、右焦点,
的左、右焦点, 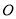 为坐标原点,点
为坐标原点,点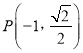 在椭圆上,线段
在椭圆上,线段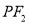 与
与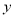 轴的交点
轴的交点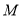 满足
满足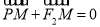 .
.(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆
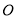 是以
是以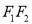 为直径的圆,一直线
为直径的圆,一直线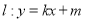 与圆
与圆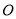 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点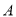 、
、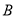 ,当
,当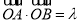 ,且满足
,且满足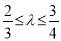 时,求
时,求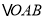 的面积
的面积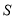 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售
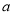 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为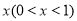 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为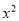 ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是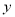 (元).
(元).(1)写出
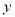 与
与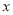 的函数关系式;
的函数关系式;(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
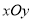 中,直线
中,直线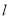 的参数方程为
的参数方程为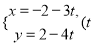 为参数).它与曲线
为参数).它与曲线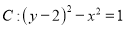 交于
交于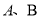 两点.
两点.(1)求
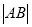 的长;
的长;(2)在以
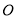 为极点,
为极点, 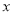 轴的正半轴为极轴建立极坐标系,设点
轴的正半轴为极轴建立极坐标系,设点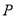 的极坐标为
的极坐标为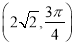 ,求点
,求点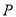 到线段
到线段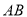 中点
中点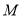 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
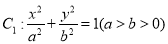 的一个焦点与抛物线
的一个焦点与抛物线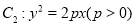 的焦点
的焦点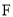 重合,且点
重合,且点 到直线
到直线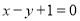 的距离为
的距离为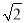 ,
, 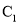 与
与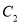 的公共弦长为
的公共弦长为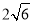 .
.(1)求椭圆
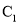 的方程及点
的方程及点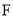 的坐标;
的坐标;(2)过点
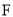 的直线
的直线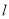 与
与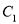 交于
交于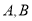 两点,与
两点,与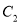 交于
交于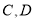 两点,求
两点,求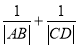 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对
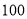 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图: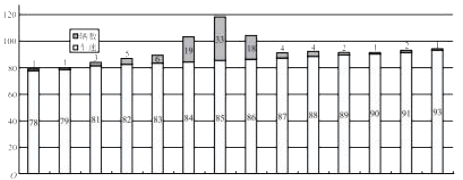
经计算:样本的平均值
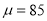 ,标准差
,标准差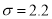 ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于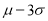 或车速大于
或车速大于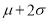 是需矫正速度.
是需矫正速度.(1)从该快速车道上所有车辆中任取
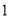 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;(2)从样本中任取
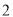 个车辆,求这
个车辆,求这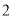 个车辆均是需矫正速度的概率;
个车辆均是需矫正速度的概率;(3)从该快速车道上所有车辆中任取
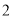 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为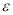 ,求
,求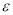 的分布列和数学期望.
的分布列和数学期望.
相关试题

