【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对![]() 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图:
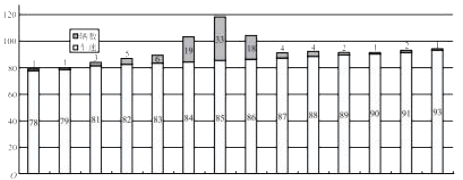
经计算:样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于![]() 或车速大于
或车速大于![]() 是需矫正速度.
是需矫正速度.
(1)从该快速车道上所有车辆中任取![]() 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;
(2)从样本中任取![]() 个车辆,求这
个车辆,求这![]() 个车辆均是需矫正速度的概率;
个车辆均是需矫正速度的概率;
(3)从该快速车道上所有车辆中任取![]() 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1) ![]() ;(2 )
;(2 ) ![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)记事件![]() 为“从该快速车道上所有车辆中任取
为“从该快速车道上所有车辆中任取![]() 个,该车辆是需矫正速度”,根据给出的条形图,即可求解事件
个,该车辆是需矫正速度”,根据给出的条形图,即可求解事件![]() 的概率;
的概率;
(2)记事件![]() 为“从样本中任取
为“从样本中任取![]() 个车辆,这
个车辆,这![]() 个车辆均是需矫正速度”根据题设,利用古典概型及其概率的计算公式,即可求解事件
个车辆均是需矫正速度”根据题设,利用古典概型及其概率的计算公式,即可求解事件![]() 概率;
概率;
(3)由题意得,需矫正速度的个数![]() 服从二项分布
服从二项分布![]() ,即可求解
,即可求解![]() 对应的概率,列出分布列,计算数学期望。
对应的概率,列出分布列,计算数学期望。
试题解析:(1)记事件![]() 为“从该快速车道上所有车辆中任取
为“从该快速车道上所有车辆中任取![]() 个,该车辆是需矫正速度”,
个,该车辆是需矫正速度”,
因为![]() ,
,
由样本条形图可知,所求的概率为
![]() .
.
(2)记事件![]() 为“从样本中任取
为“从样本中任取![]() 个车辆,这
个车辆,这![]() 个车辆均是需矫正速度”
个车辆均是需矫正速度”
由题设可知样本容量为![]() ,又需矫正速度个数为
,又需矫正速度个数为![]() 个,故所求概率为
个,故所求概率为![]() .
.
(3)需矫正速度的个数![]() 服从二项分布,即
服从二项分布,即![]() ,
,
∴![]() ,
, ![]() ,
,
![]() ,
,
因此![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
由![]() ,知数学期望
,知数学期望![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
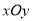 中,曲线
中,曲线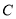 的参数方程为
的参数方程为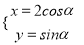 (
(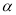 为参数),在以原点为极点,
为参数),在以原点为极点, 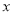 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线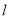 的极坐标方程为
的极坐标方程为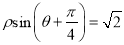 .
.(1)求
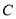 的普通方程和
的普通方程和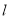 的倾斜角;
的倾斜角;(2)设点
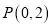 ,
, 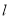 和
和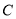 交于
交于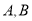 两点,求
两点,求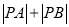 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
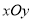 中,直线
中,直线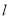 的参数方程为
的参数方程为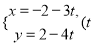 为参数).它与曲线
为参数).它与曲线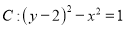 交于
交于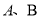 两点.
两点.(1)求
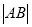 的长;
的长;(2)在以
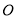 为极点,
为极点, 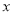 轴的正半轴为极轴建立极坐标系,设点
轴的正半轴为极轴建立极坐标系,设点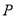 的极坐标为
的极坐标为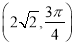 ,求点
,求点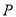 到线段
到线段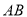 中点
中点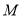 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
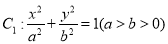 的一个焦点与抛物线
的一个焦点与抛物线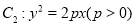 的焦点
的焦点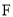 重合,且点
重合,且点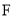 到直线
到直线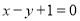 的距离为
的距离为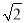 ,
, 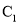 与
与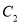 的公共弦长为
的公共弦长为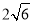 .
.(1)求椭圆
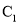 的方程及点
的方程及点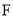 的坐标;
的坐标;(2)过点
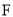 的直线
的直线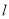 与
与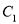 交于
交于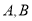 两点,与
两点,与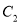 交于
交于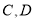 两点,求
两点,求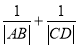 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年入冬以来,各地雾霾天气频发,
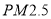 频频爆表(
频频爆表(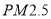 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与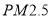 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与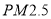 的数据如下表:
的数据如下表:时间
周一
周二
周三
周四
周五
车流量
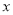 (万辆)
(万辆)50
51
54
57
58
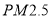 的浓度
的浓度 (微克/立方米)
(微克/立方米)69
70
74
78
79
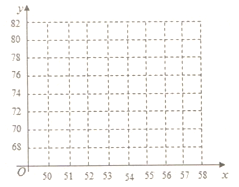
(1)请根据上述数据,在下面给出的坐标系中画出散点图;
(2)试判断
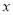 与
与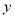 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出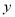 关于
关于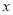 的线性回归方程
的线性回归方程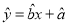 ,若没有,请说明理由;
,若没有,请说明理由;(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的
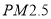 的浓度(保留整数).
的浓度(保留整数).参考公式:
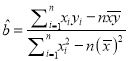
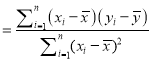 ,
, 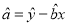 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
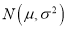 .
.(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在
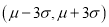
之外的零件数,求
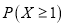 ;
;(2)一天内抽检零件中,如果出现了尺寸在
 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.下面是检验员在一天内抽取的16个零件的尺寸:
9.95
10.12
9.96
9.96
10.01
9.92
9.98
10.04
10.26
9.91
10.13
10.02
9.22
10.04
10.05
9.95
经计算得
 ,
, 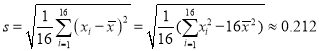 ,其中
,其中 为抽取的第
为抽取的第 个零件的尺寸,
个零件的尺寸,  .
.用样本平均数
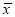 作为
作为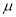 的估计值
的估计值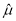 ,用样本标准差
,用样本标准差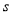 作为
作为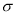 的估计值
的估计值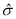 ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除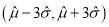 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计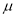 和
和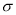 (精确到0.01).
(精确到0.01).附:若随机变量
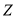 服从正态分布
服从正态分布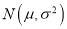 ,则
,则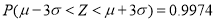 ,
,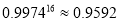 ,
, 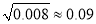 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期
12月1日
12月2日
12月3日
12月4日
12月5日
温差x (℃)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
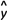 =
=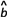 x+
x+ ;
;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
附:
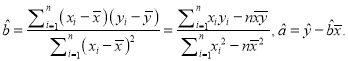
相关试题

