【题目】已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,公差
,公差![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() ;数列
;数列![]() 满足:对于任意的
满足:对于任意的![]() ,等式
,等式![]() 都成立.
都成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 满足
满足![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有满足条件的数组
成等比数列?若存在,求出所有满足条件的数组![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】分析:(1)根据已知解方程组得![]() ,即得数列
,即得数列![]() 的通项公式.(2)利用作差法化简
的通项公式.(2)利用作差法化简
![]() 即得
即得![]() ,即证明数列
,即证明数列![]() 是等比数列.(3)先化简
是等比数列.(3)先化简![]() ,再化简
,再化简![]() ,
,![]() ,
,![]() 成等比数列,对s分类讨论得解.
成等比数列,对s分类讨论得解.
详解:(1)设数列![]() 公差为
公差为![]() ,由题设得
,由题设得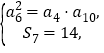
即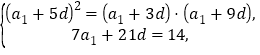 解得
解得![]()
∴数列![]() 的通项公式为:
的通项公式为:![]() .
.
(2)∵![]()
∴![]() ,①
,①
∴![]() ,②
,②
由②-①得![]() ,③
,③
∴![]() ,④
,④
由④-③得![]() ,
,
由①知![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴数列
,∴数列![]() 是等比数列.
是等比数列.
(3)假设存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
由(2)可知:![]() ,∴
,∴![]() .
.
于是,![]() .
.
由于![]() ,所以
,所以![]()
因为当![]() 时,
时,![]() ,即
,即![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() ,不符合条件,
,不符合条件,
所以![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]()
当![]() 时,得
时,得![]() ,无解,
,无解,
当![]() 时,得
时,得![]() ,所以
,所以![]() ,
,
综上:存在唯一正整数数组![]() ,使
,使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某单位用2160万元购得一块空地,计划在该空地上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为
 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).
(单位:元).(1)写出楼房每平方米的平均综合费用
 关于建造层数
关于建造层数 的函数关系式;
的函数关系式;(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰
是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰 米,
米, .为了给市民营造良好的休闲环境,公园管理处决定在湖岸
.为了给市民营造良好的休闲环境,公园管理处决定在湖岸 ,
, 上分别取点
上分别取点 ,
, (异于线段端点),在湖上修建一条笔直的水上观光通道
(异于线段端点),在湖上修建一条笔直的水上观光通道 (宽度不计),使得三角形
(宽度不计),使得三角形 和四边形
和四边形 的周长相等.
的周长相等. 
(1)若水上观光通道的端点
 为线段
为线段 的三等分点(靠近点
的三等分点(靠近点 ),求此时水上观光通道
),求此时水上观光通道 的长度;
的长度;(2)当
 为多长时,观光通道
为多长时,观光通道 的长度最短?并求出其最短长度.
的长度最短?并求出其最短长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解关于
 的不等式
的不等式 ;
;(2)若当
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论不正确的是________(填序号).
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)分析,你认为选派哪位学生参加合适?请说明理由
参考公式:

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
相关试题

