【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
参考答案:
【答案】见解析
【解析】(1)设数列{an}的公差为d.
因为a1=1,且a1,a2,a5依次成等比数列,
所以a=a1·a5,即(1+d)2=1·(1+4d),
所以d2-2d=0,解得d=2(d=0不合要求,舍去).
所以an=1+2(n-1)=2n-1.
因为bn+1=2bn-1,所以bn+1-1=2(bn-1).
所以{bn-1}是首项为b1-1=2,公比为2的等比数列.
所以bn-1=2×2n-1=2n.
所以bn=2n+1.
(2)因为![]() =
=![]() =
=![]() -
-![]() ,
,
所以Sn=![]() +
+![]() +…+
+…+![]() =1-
=1-![]() ,
,
于是Sn-![]() =1-
=1-![]() -1+
-1+![]() =
=![]() -
-![]() =
=![]() .
.
所以当n=1,2时,2n=2n,Sn=1-![]() ;
;
当n≥3时,2n<2n,Sn<1-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:
女
47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49
男
37 35 34 43 46 36 38 40 39 32 48 33 40 34
(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数
“不满意”的人数
合计
女
16
男
14
合计
30
(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:

0.10
0.050
0.025
0.010
0.001

2.706
3.841
5.024
6.635
10.828
参考公式:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某几何体的三视图,则该几何体的体积为( )
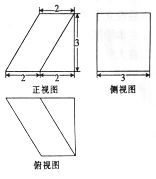
A. 12 B. 15 C. 18 D. 21
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,直线
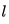 的参数方程为
的参数方程为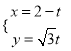 (t为参数),P、Q分别为直线
(t为参数),P、Q分别为直线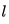 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.(Ⅰ)求直线
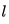 的直角坐标方程;
的直角坐标方程;(Ⅱ)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
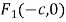 、
、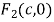 分别是椭圆
分别是椭圆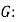
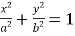
 的左、右焦点,点
的左、右焦点,点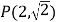 是椭圆
是椭圆 上一点,且
上一点,且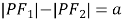 .
.(1)求椭圆
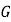 的方程;
的方程;(2)设直线
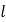 与椭圆
与椭圆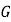 相交于
相交于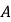 ,
,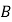 两点,若
两点,若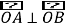 ,其中
,其中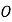 为坐标原点,判断
为坐标原点,判断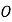 到直线
到直线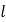 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
相关试题

