【题目】函数f(x)=sin(ωx+φ)( ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
参考答案:
【答案】C
【解析】解:由题意可得 ![]() =π,解得ω=2,故函数f(x)=sin(2x+φ),其图象向右平移
=π,解得ω=2,故函数f(x)=sin(2x+φ),其图象向右平移 ![]() 个单位后得到的图象对应的函数为 y=sin[2(x﹣
个单位后得到的图象对应的函数为 y=sin[2(x﹣ ![]() )+φ]=sin(2x﹣
)+φ]=sin(2x﹣ ![]() +φ]是奇函数,故φ=﹣
+φ]是奇函数,故φ=﹣ ![]() ,
,
故 函数f(x)=sin(2x﹣ ![]() ),故当
),故当 ![]() 时,函数f(x)=sin
时,函数f(x)=sin ![]() =1,故函数f(x)=sin(2x﹣
=1,故函数f(x)=sin(2x﹣ ![]() ) 关于直线
) 关于直线 ![]() 对称,
对称,
故选C.
【考点精析】本题主要考查了正弦函数的奇偶性和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握正弦函数为奇函数;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
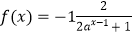 (a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(Ⅱ) 证明函数f(x)在R上是增函数;
(Ⅲ)当x∈[1,+∞)时,mf(x)≤2x﹣2恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆柱
 底面半径为1,高为
底面半径为1,高为 ,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线
,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线 如图所示.将轴截面ABCD绕着轴
如图所示.将轴截面ABCD绕着轴 逆时针旋转
逆时针旋转 后,边
后,边 与曲线
与曲线 相交于点P.
相交于点P.(Ⅰ)求曲线
 长度;
长度;(Ⅱ)当
 时,求点
时,求点 到平面APB的距离;
到平面APB的距离;(Ⅲ)证明:不存在
 ,使得二面角
,使得二面角 的大小为
的大小为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
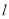 :
: 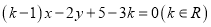 恒过定点
恒过定点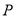 ,圆
,圆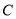 经过点
经过点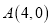 和点
和点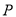 ,且圆心在直线
,且圆心在直线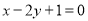 上.
上.(1)求定点
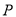 的坐标;
的坐标;(2)求圆
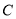 的方程;
的方程;(3)已知点
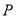 为圆
为圆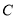 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点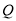 ,问:在
,问:在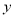 轴上是否存在一点
轴上是否存在一点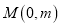 ,使得
,使得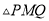 为直角三角形,若存在,求出
为直角三角形,若存在,求出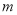 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.

(1)当θ=
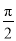 时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;
时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;(2)当θ=
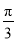 时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.
时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆过定点
 ,且在
,且在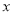 轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.(Ⅰ)求直线
 与曲线C围成的区域面积;
与曲线C围成的区域面积; (Ⅱ)点
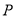 在直线
在直线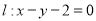 上,点
上,点 ,过点
,过点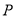 作曲线C的切线
作曲线C的切线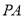 、
、 ,切点分别为
,切点分别为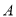 、
、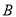 ,证明:存在常数
,证明:存在常数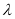 ,使得
,使得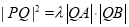 ,并求
,并求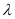 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A1,∠A2,…,∠An为凸多边形的内角,且lg sin A1+lg sin A2+…+lg sin An=0,则这个多边形是( )
A. 正六边形 B. 梯形
C. 矩形 D. 含锐角的菱形
相关试题

