【题目】已知直线l1经过点A(﹣3,0),B(3,2),直线l2经过点B,且l1⊥l2 .
(1)求经过点B且在两坐标轴上的截距相等的直线的方程;
(2)设直线l2与直线y=8x的交点为C,求△ABC外接圆的方程.
参考答案:
【答案】
(1)解:设经过点B且在两坐标轴上的截距相等的直线为m,
①当直线m经过原点时,在两坐标轴上的截距都为零,符合题意.
此时,直线m的方程为y= ![]() x;
x;
②当直线m不经过原点时,设方程为 ![]() ,
,
将点B(3,2)代入,得 ![]() ,解之得a=5,
,解之得a=5,
此时直线m的方程为 ![]() ,化简得x+y﹣5=0.
,化简得x+y﹣5=0.
综上所述,直线m方程为y= ![]() x或x+y﹣5=0,即为所求直线的方程
x或x+y﹣5=0,即为所求直线的方程
(2)解:∵直线l1经过点A(﹣3,0),B(3,2),
∴直线l1的斜率k1= ![]() =
= ![]() ,
,
∵l1⊥l2,∴直线l2的斜率k2= ![]() =﹣3.
=﹣3.
又∵直线l2经过点B(3,2),
∴直线l2的方程为y﹣2=﹣3(x﹣3),即y=﹣3x+11,
由 ![]() 联解,得
联解,得 ![]() ,可得直线l2与直线y=8x的交点为C(1,8).
,可得直线l2与直线y=8x的交点为C(1,8).
设经过A、B、C三点的圆方程为x2+y2+Dx+Ey+F=0,
可得 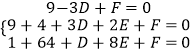 ,解之得
,解之得 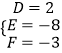 ,
,
∴经过A、B、C三点的圆方程为x2+y2+2x﹣8y﹣3=0,即为△ABC外接圆的方程
【解析】(1)根据直线经过原点或不经过原点,分两种情况加以讨论,利用直线在坐标轴上截距的概念和直线方程的截距式,即可算出满足条件的直线方程;(2)由A、B的坐标算出直线l1的斜率k1= ![]() ,从而得到l2的斜率k2=
,从而得到l2的斜率k2= ![]() =﹣3,利用点斜式列式可得直线l2的方程为y=﹣3x+11.联解直线l2与直线y=8x,算出交点为C(1,8),设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,代入A、B、C的坐标解出D、E、F的值,即可得到所求△ABC外接圆的方程.
=﹣3,利用点斜式列式可得直线l2的方程为y=﹣3x+11.联解直线l2与直线y=8x,算出交点为C(1,8),设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,代入A、B、C的坐标解出D、E、F的值,即可得到所求△ABC外接圆的方程.
【考点精析】解答此题的关键在于理解截距式方程的相关知识,掌握直线的截距式方程:已知直线![]() 与
与![]() 轴的交点为A
轴的交点为A![]() ,与
,与![]() 轴的交点为B
轴的交点为B![]() ,其中
,其中![]() ,以及对圆的标准方程的理解,了解圆的标准方程:
,以及对圆的标准方程的理解,了解圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设圆
 的圆心在
的圆心在 轴上,并且过
轴上,并且过 两点.
两点.(1)求圆
 的方程;
的方程;(2)设直线
 与圆
与圆 交于
交于 两点,那么以
两点,那么以 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线 的方程;若不能,请说明理由.
的方程;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
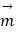 =(
=( 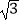 sinx,2),
sinx,2), 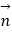 =(2cosx,cos2x),函数f(x)=
=(2cosx,cos2x),函数f(x)= 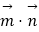 ,
,
(1)求函数f(x)的值域;
(2)在△ABC中,角A,B,C和边a,b,c满足a=2,f(A)=2,sinB=2sinC,求边c. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
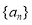 为等差数列,前n项和为
为等差数列,前n项和为 ,
, 是首项为2的等比数列,且公比大于0,
是首项为2的等比数列,且公比大于0, ,
, ,
,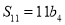 .
.(1)求
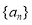 和
和 的通项公式;
的通项公式;(2)求数列
 的前n项和
的前n项和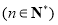 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,
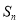 为前
为前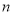 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则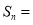 _________________尺.
_________________尺. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
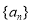 满足
满足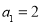 ,
,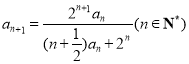 .
.(1)设
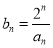 ,求数列
,求数列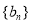 的通项公式;
的通项公式;(2)设
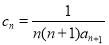 ,求数列
,求数列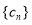 的前n项和为
的前n项和为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了
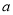 ,
, 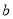 ,
, 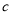 ,
, 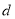 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是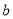 ,3号门里是
,3号门里是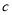 ;乙同学说:2号门里是
;乙同学说:2号门里是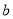 ,3号门里是
,3号门里是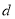 ;丙同学说:4号门里是
;丙同学说:4号门里是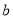 ,2号门里是
,2号门里是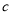 ;丁同学说:4号门里是
;丁同学说:4号门里是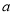 ,3号门里是
,3号门里是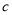 .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )A.
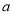 B.
B. 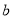 C.
C. 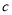 D.
D. 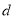
相关试题

