【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,![]() (1+x)
(1+x) ![]() <e.
<e.
参考答案:
【答案】见解析
【解析】(1)f′(x)=![]() -a,函数f(x)=ln x-ax的定义域为(0,+∞),
-a,函数f(x)=ln x-ax的定义域为(0,+∞),
当a≤0时,f′(x)>0,此时f(x)在(0,+∞)上是增函数,
当a>0时,x∈![]() 时,f′(x)>0,此时f(x)在
时,f′(x)>0,此时f(x)在![]() 上是增函数,x∈
上是增函数,x∈![]() 时,f′(x)<0,此时f(x)在
时,f′(x)<0,此时f(x)在![]() 上是减函数.
上是减函数.
综上,当a≤0时,f(x)在(0,+∞)上是增函数,当a>0时,f(x)在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(2)f(x)<0在(0,+∞)上恒成立,即a>![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
设g(x)=![]() ,则g′(x)=
,则g′(x)=![]() ,
,
当x∈(0,e)时,g′(x)>0,g(x)为增函数,当x∈(e,+∞)时,g′(x)<0,g(x)为减函数,
故当x=e时,g(x)取得最大值![]() ,
,
所以a的取值范围是![]() .
.
(3)证明:要证当x∈(0,+∞)时,![]() (1+x)
(1+x) ![]() <e,设t=1+x,t∈(1,+∞),只要证t
<e,设t=1+x,t∈(1,+∞),只要证t![]() <et,两边取以e为底数的对数,即ln t<t-1.
<et,两边取以e为底数的对数,即ln t<t-1.
由(1)知当a=1时,f(x)=ln x-x的最大值为-1,此时x=1,所以当t∈(1,+∞)时,ln t-t<-1,
即得ln t<t-1,所以原不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第
 个等式为 .
个等式为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行的“国际马拉松赛”,举办单位在活动推介晚会上进行嘉宾现场抽奖活动,抽奖盒中装有6个大小相同的小球,分别印有“快乐马拉松”和“美丽绿城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球(取出后不再放回),若抽到的两个球都印有“快乐马拉松”标志即可获奖.并停止取球;否则继续抽取,第一次取球就抽中获一等奖,第二次取球抽中获二等奖,第三次取球抽中获三等奖,没有抽中不获奖.活动开始后,一位参赛者问:“盒中有几个印有‘快乐马拉松’的小球?”主持人说:“我只知道第一次从盒中同时抽两球,不都是‘美丽绿城行’标志的概率是
(1)求盒中印有“快乐马拉松”小球的个数;
(2)若用
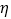 表示这位参加者抽取的次数,求
表示这位参加者抽取的次数,求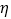 的分布列及期望.
的分布列及期望. -
科目: 来源: 题型:
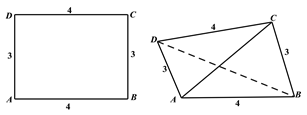
查看答案和解析>>【题目】已知矩形
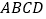 的长
的长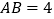 ,宽
,宽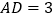 ,将其沿对角线
,将其沿对角线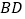 折起,得到四面体
折起,得到四面体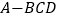 ,
,如图所示,给出下列结论:
①四面体
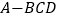 体积的最大值为
体积的最大值为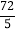 ;
;②四面体
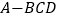 外接球的表面积恒为定值;
外接球的表面积恒为定值;③若
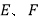 分别为棱
分别为棱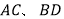 的中点,则恒有
的中点,则恒有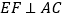 且
且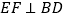 ;
; ④当二面角
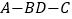 为直二面角时,直线
为直二面角时,直线 所成角的余弦值为
所成角的余弦值为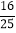 ;
;⑤当二面角
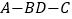 的大小为
的大小为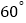 时,棱
时,棱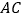 的长为
的长为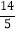 .
.
其中正确的结论有____________________(请写出所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
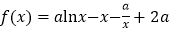 (其中
(其中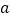 为常数,
为常数,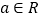 ).(Ⅰ)求函数
).(Ⅰ)求函数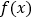 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当 时,是否存在实数
时,是否存在实数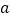 ,使得当
,使得当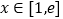 时,不等式
时,不等式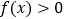 恒成立?如果存在,求
恒成立?如果存在,求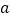 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中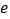 是自然对数的底数,
是自然对数的底数,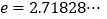 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】截止到1999年底,我国人口约为13亿,若今后能将人口平均增长率控制在1%,经过x年后,我国人口为y(单位:亿).
(1)求y与x的函数关系式y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数,并指出函数增减的实际意义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察以下5个等式:
-1=-1
-1+3=2
-1+3-5=-3
-1+3-5+7=4
-1+3-5+7-9=-5
……
根据以上式子规律:
(1)写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
相关试题

