【题目】已知椭圆 ![]() (a>b>0)右顶点与右焦点的距离为
(a>b>0)右顶点与右焦点的距离为 ![]() ﹣1,短轴长为2
﹣1,短轴长为2 ![]() .
.
(1)求椭圆的方程;
(2)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为 ![]() ,求直线AB的方程.
,求直线AB的方程.
参考答案:
【答案】
(1)解:由题意, 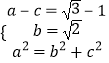 ,解得
,解得 ![]() .
.
即椭圆方程为 ![]()
(2)解:当直线AB与x轴垂直时, ![]() ,此时
,此时 ![]() 不符合题意,故舍掉;
不符合题意,故舍掉;
当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得:(2+3k2)x2+6k2x+(3k2﹣6)=0.
设A(x1,y1),B(x2,y2),则 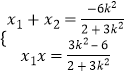 ,所以
,所以 ![]() .
.
原点到直线的AB距离 ![]() ,
,
所以三角形的面积 ![]() .
.
由 ![]() 可得k2=2,∴
可得k2=2,∴ ![]() ,
,
所以直线 ![]() 或
或 ![]()
【解析】(1)根据椭圆右顶点与右焦点的距离为 ![]() -1,短轴长为2
-1,短轴长为2 ![]() ,可得
,可得 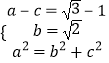 ,由此,即可求得椭圆方程;(2)当直线AB与x轴垂直时,
,由此,即可求得椭圆方程;(2)当直线AB与x轴垂直时, ![]() ,此时
,此时 ![]() 不符合题意;当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得,进而可求三角形的面积,利用
不符合题意;当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得,进而可求三角形的面积,利用 ![]() ,即可求出直线AB的方程.
,即可求出直线AB的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下列联表:
喜欢户外运动
不喜欢户外运动
合计
男性
5
女性
10
合计
50
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是
 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由;
(3)经进一步调查发现,在喜欢户外运动的10名女性员工中,有4人还喜欢瑜伽.若从喜欢户外运动的10位女性员工中任选3人,记ξ表示抽到喜欢瑜伽的人数,求ξ的分布列和数学期望.
下面的临界值表仅供参考:P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  分别是
分别是 的中点.
的中点.(1)求证: 平面
 平面
平面 ;
;(2)求证:
 平面
平面 ;
;(3)求三棱锥
 体积.
体积.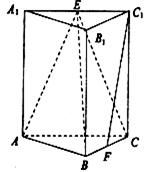
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥B﹣ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.

(1)求证:BE⊥DF;
(2)求二面角B﹣DE﹣F的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 分)如图,在三棱锥
分)如图,在三棱锥 中,底面
中,底面 为等边三角形,
为等边三角形, ,
, ,
, 为
为 的中点.
的中点.(Ⅰ)求证:
 .
.(Ⅱ)判断在线段
 上是否存在点
上是否存在点 (与点
(与点 不重合),使得
不重合),使得 为直角三角形?若存在,试找出一个点
为直角三角形?若存在,试找出一个点 ,并求
,并求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ﹣lnx.
﹣lnx.
(1)若f(x)在x=3处取得极值,求实数a的值;
(2)若f(x)≥5﹣3x恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①残差可用来判断模型拟合的效果;
②设有一个回归方程
 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;③线性回归方程
 必过
必过 ;
;④在一个2×2列联表中,由计算得
 =13.079,则有99%的把握确认这两个变量间有关系(其中
=13.079,则有99%的把握确认这两个变量间有关系(其中 );
);其中错误的个数是( )
A. 0 B. 1 C. 2 D. 3.
相关试题

