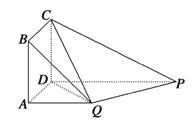
【题目】如图,四边形![]() 为正方形,
为正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .试结合向量法:(1)证明:平面
.试结合向量法:(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:首先根据题意以![]() 为坐标原点,线段
为坐标原点,线段![]() 的长为单位长,射线
的长为单位长,射线![]() 为
为![]() 轴正半轴建立空间直角坐标系
轴正半轴建立空间直角坐标系![]() ;(1)根据坐标系,求出
;(1)根据坐标系,求出![]() 、
、![]() 、
、![]() 的坐标,由向量积的运算易得
的坐标,由向量积的运算易得![]() ,
, ![]() ,进而可得
,进而可得![]() ,
, ![]() ,由面面垂直的判定,即可证明;(2)依题意结合坐标系,可得
,由面面垂直的判定,即可证明;(2)依题意结合坐标系,可得![]() 、
、![]() 、
、![]() 的坐标,进而求出平面
的坐标,进而求出平面![]() 与平面
与平面![]() 的法向量,根据二面角与其法向量夹角的关系,即可得答案.
的法向量,根据二面角与其法向量夹角的关系,即可得答案.
试题解析:如图,以![]() 为坐标原点,线段
为坐标原点,线段![]() 的长为单位长,射线
的长为单位长,射线![]() 为
为![]() 轴正半轴建立空间直角坐标系
轴正半轴建立空间直角坐标系![]() .
.
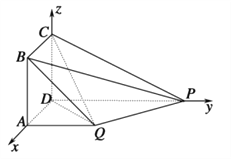
(1)证明:依题意有![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,即
,即![]() ,
, ![]() .
.
∴![]() 平面
平面![]()
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
(2)依题意有![]() ,
, ![]() ,
, ![]()
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
![]() ,即
,即![]()
∴可取![]()
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
![]() 可取
可取![]()
∴![]() ,则二面角
,则二面角![]() 的余弦值为
的余弦值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
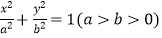 的离心率为
的离心率为 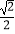 ,右焦点为F,点B(0,1)在椭圆C上.
,右焦点为F,点B(0,1)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 的直线交椭圆C于M,N两点,交直线x=2于点P,设
的直线交椭圆C于M,N两点,交直线x=2于点P,设  ,
, 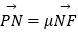 ,求证:λ+μ为定值.
,求证:λ+μ为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知a=bcosC+
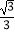 csinB.
csinB.
(1)若a=2,b= ,求c
,求c
(2)设函数y=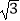 sin(2A﹣30°)﹣2sin2(C﹣15°),求y的取值范围.
sin(2A﹣30°)﹣2sin2(C﹣15°),求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜三棱柱ABC﹣A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.

(1)求证:平面ACC1A1⊥平面B1C1CB;
(2)若二面角B﹣AB1﹣C1的余弦值为 ,求斜三棱柱ABC﹣A1B1C1的侧棱AA1的长度.
,求斜三棱柱ABC﹣A1B1C1的侧棱AA1的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于n∈N* , 若数列{xn}满足xn+1﹣xn>1,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数m的取值范围;
(Ⅱ)是否存在首项为﹣1的等差数列{an}为“K数列”,且其前n项和Sn满足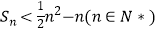 ?若存在,求出{an}的通项公式;若不存在,请说明理由;
?若存在,求出{an}的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列{an}是“K数列”,数列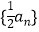 不是“K数列”,若
不是“K数列”,若 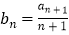 ,试判断数列{bn}是否为“K数列”,并说明理由.
,试判断数列{bn}是否为“K数列”,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=2
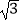 cos2x﹣2sinxcosx﹣
cos2x﹣2sinxcosx﹣ 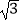 的图象向左平移t(t>0)个单位,所得图象对应的函数为奇函数,则t的最小值为( )
的图象向左平移t(t>0)个单位,所得图象对应的函数为奇函数,则t的最小值为( )
A.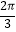
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有2500名学生,其中高一1000人,高二900人,高三600人,为了了解学生的身体健康状况,采用分层抽样的方法,若从本校学生中抽取100人,从高一和高三抽取样本数分别为a,b,且直线ax+by+8=0与以A(1,﹣1)为圆心的圆交于B,C两点,且∠BAC=120°,则圆C的方程为( )
A.(x﹣1)2+(y+1)2=1
B.(x﹣1)2+(y+1)2=2
C.(x﹣1)2+(y+1)2=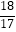
D.(x﹣1)2+(y+1)2=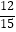
相关试题

