【题目】某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对![]() 两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
| 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从![]() 类样本中任选一人,求此人属于中低消费人群的概率;
类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从![]() 两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计![]() 两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
参考答案:
【答案】(1)0.7;(2)0.78;(3)B.
【解析】试题分析:
(Ⅰ)利用题意结合古典概型公式可得从![]() 类样本中任选一人,求此人属于中低消费人群的概率为0.7;
类样本中任选一人,求此人属于中低消费人群的概率为0.7;
(Ⅱ)利用题意列出所有可能的时间,然后进行计算可得甲的消费档次不低于乙的消费档次的概率为0.78
(Ⅲ)利用题中数据的波动程度可得![]() 两类人群哪类月均服装消费额的方差较大是B.
两类人群哪类月均服装消费额的方差较大是B.
试题解析:
(Ⅰ)设此人属于中低消费人群为事件![]() ,
,
则 ![]()
![]()
(Ⅱ)设甲的消费档次不低于乙的消费档次为事件![]() ,
,
则 ![]()
![]()
![]()
(Ⅲ)答:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
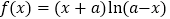 .
.(Ⅰ)当
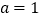 时,求曲线
时,求曲线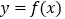 在
在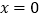 处的切线方程;
处的切线方程;(Ⅱ)当
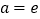 时,求证:函数
时,求证:函数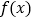 在
在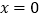 处取得最值.
处取得最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|x2﹣3x﹣4<0,x∈Z}用列举法表示为
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的方程x2+px﹣12=0和x2+qx+r=0的解集分别是A,B,且A≠B.A∪B={﹣3,2,4},A∩B={﹣3}.求p,q,r的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
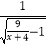 的定义域为集合A,集合B={x||x+2|+|x﹣2|>8}.
的定义域为集合A,集合B={x||x+2|+|x﹣2|>8}.
(1)求集合A,B;
(2)求B∩∪A. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆:

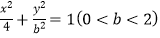 , 左右焦点分别为F1 , F2 , 过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是
, 左右焦点分别为F1 , F2 , 过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司一年经销某种商品,年销售量400吨,每吨进价5万元,每吨销售价8万元.全年进货若干次,每次都购买x吨,运费为每次2万元,一年的总存储费用为2x万元.
(1)求该公司经销这种商品一年的总利润y与x的函数关系;
(2)要使一年的总利润最大,则每次购买量为多少?并求出最大利润.
相关试题

