【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且方程
,且方程![]() 在
在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(2)
.(2)![]()
【解析】【试题分析】(1)先求出函数解析式导数,再借助导数与函数的单调性的关系求解;(2)依据题设先将问题进行等价转化,再构造函数运用导数与函数的单调性的关系研究函数的图像的形状分析求解:
(1)若![]() ,
, ![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
①若![]() ,即
,即![]() 时,
时, ![]() ,此时函数单调递减,单调递减区间为
,此时函数单调递减,单调递减区间为![]() ;
;
②若![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() 得
得![]() ,或
,或![]() ,
,
所以单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)若![]() ,∴
,∴![]() ,
, ![]() 则,
则,
若方程![]() 在
在![]() 内有解,即
内有解,即![]() 在
在![]() 内有解,
内有解,
即![]() 在
在![]() 有解.
有解.
设![]() ,则
,则![]() 在
在![]() 内有零点,设
内有零点,设![]() 是
是![]() 在
在![]() 内的一个零点,
内的一个零点,
因为![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上不可能单调,
上不可能单调,
由![]() ,设
,设![]() ,则
,则![]() 在
在![]() 和
和![]() 上存在零点,
上存在零点,
即![]() 在
在![]() 上至少有两个零点,因为
上至少有两个零点,因为![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递增,不合题意;
上递增,不合题意;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,不合题意;
上递减,不合题意;
当![]() 时,令
时,令![]() ,得
,得![]() ,则
,则![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
![]() 在
在![]() 上存在最小值
上存在最小值![]() .
.
若![]() 有两个零点,则有
有两个零点,则有![]() ,
, ![]() .
.
所以![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递减,
递减,
则![]() ,所以
,所以![]() 恒成立.
恒成立.
由![]() ,
, ![]() ,所以
,所以![]() ,
,
当![]() 时,设
时,设![]() 的两个零点为
的两个零点为![]() ,
,
则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
则![]() ,
, ![]() ,则
,则![]() 在
在![]() 内有零点,
内有零点,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方体
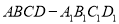 中,
中, 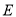 ,
, 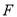 分别是
分别是 ,
, 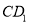 的中点,
的中点,  ,
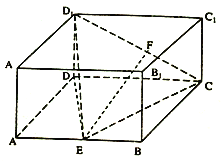
, 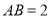 .
.
(Ⅰ)求证:
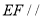 平面
平面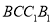 ;
;(Ⅱ)求证:平面
 平面
平面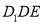 ;
;(Ⅲ)在线段
 上是否存在一点
上是否存在一点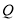 ,使得二面角
,使得二面角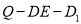 为
为 ,若存在,求
,若存在,求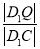 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
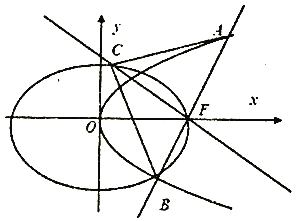
查看答案和解析>>【题目】如图,设椭圆
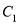 :
: 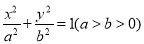 ,长轴的右端点与抛物线
,长轴的右端点与抛物线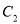 :
: 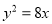 的焦点
的焦点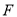 重合,且椭圆
重合,且椭圆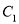 的离心率是
的离心率是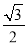 .
.
(Ⅰ)求椭圆
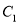 的标准方程;
的标准方程;(Ⅱ)过
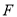 作直线
作直线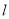 交抛物线
交抛物线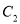 于
于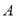 ,
, 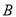 两点,过
两点,过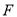 且与直线
且与直线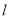 垂直的直线交椭圆
垂直的直线交椭圆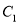 于另一点
于另一点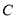 ,求
,求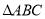 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线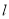 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】第32届夏季奥林匹克运动会将于2020年在日本东京举行,下表是五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届伦敦
第29届北京
第28届雅典
第27届悉尼
第26届亚特兰大
中国
38
51
32
28
16
俄罗斯
24
23
27
32
26
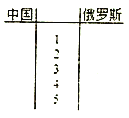
(Ⅰ)根据表格中两组数据完成五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(Ⅱ)甲、乙、丙三人竞猜2020年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为
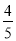 ,丙猜中中国代表团的概率为
,丙猜中中国代表团的概率为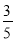 ,三人各自猜哪个代表团的结果互不影响,现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为
,三人各自猜哪个代表团的结果互不影响,现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为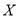 ,求
,求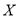 的分布列及数学期望
的分布列及数学期望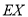 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三数学竞赛初赛考试后,对部分考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,若第四、五、六组的人数依次成等差数列,且第六组有4人.

(1)请补充完整频率分布直方图,并估计这组数据的平均数M;
(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为
 .若
.若 ,则称此二人为“黄金帮扶组”.试求选出的二人为“黄金帮扶组”的概率
,则称此二人为“黄金帮扶组”.试求选出的二人为“黄金帮扶组”的概率 ;
;(3)以此样本的频率当做概率,现随机在这所有考生中选出3名学生,求成绩不低于120分的人数
 的分布列及期望.
的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
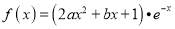 (
(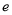 为自然对数的底数).
为自然对数的底数).(1)若
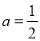 ,
, 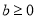 ,求函数
,求函数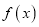 的单调区间;
的单调区间;(2)若
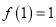 ,且方程
,且方程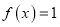 在
在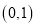 内有解,求实数
内有解,求实数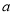 的取值范围.
的取值范围.
相关试题

