【题目】定义:圆心到直线的距离与圆的半径之比为直线关于圆的距离比![]() .
.
(1)设圆![]() 求过
求过![]() (2,0)的直线关于圆
(2,0)的直线关于圆![]() 的距离比
的距离比![]() 的直线方程;
的直线方程;
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() (0,3)且直线
(0,3)且直线![]() =
= ![]() 关于圆
关于圆![]() 的距离比
的距离比![]() ,求此圆的
,求此圆的![]() 的方程;
的方程;
(3)是否存在点![]() ,使过
,使过![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 的距离比始终相等?若存在,求出相应的点
的距离比始终相等?若存在,求出相应的点![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在
;(3)存在![]() .
.
【解析】试题分析:(1)设过![]() 的直线方程为
的直线方程为![]() ,求得已知圆的圆心和半径,由新定义,可得方程,求得
,求得已知圆的圆心和半径,由新定义,可得方程,求得![]() ,即可得到所求直线方程;(2)设圆
,即可得到所求直线方程;(2)设圆![]() 的方程为
的方程为![]() ,由题意可得
,由题意可得![]() ,解方程可得
,解方程可得![]() ,
, ![]() ,
, ![]() ,进而得到所求圆的方程;(3)假设存在点
,进而得到所求圆的方程;(3)假设存在点![]() ,设过
,设过![]() 的两直线为
的两直线为![]() 和
和![]() ,求得两圆的圆心和半径,由新定义可得方程,化简整理可得
,求得两圆的圆心和半径,由新定义可得方程,化简整理可得![]() 或
或![]() ,再由恒成立思想可得
,再由恒成立思想可得![]() ,
, ![]() 的方程,解方程可得
的方程,解方程可得![]() 的坐标.
的坐标.
试题解析:(1)设过![]() 的直线方程为
的直线方程为![]()
∵圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]()
∴根据题意可得![]()
∴![]() ,即所求直线为
,即所求直线为![]() ;
;
(2)设圆![]() 的方程为
的方程为![]()
根据题意可得![]()
∴解方程可得![]() 或
或![]() ,则有圆
,则有圆![]() 的方程为
的方程为![]() 或
或![]()
(3)假设存在点![]() ,设过
,设过![]() 的两直线为
的两直线为![]() 和
和![]()
又∵![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
, ![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]()
∴根据题意可得 ,即
,即![]() 或
或![]()
∴![]() 或
或![]() ,
,
∴![]() 或
或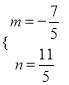 ,则存在这样的点
,则存在这样的点![]() 和
和![]() ,使得使过
,使得使过![]() 的任意两条互相垂直的直线分别关于相应两圆的距离比始终相等.
的任意两条互相垂直的直线分别关于相应两圆的距离比始终相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入
 (单位:万元)满足
(单位:万元)满足 ,乙城市收益Q与投入
,乙城市收益Q与投入 (单位:万元)满足
(单位:万元)满足 ,设甲城市的投入为
,设甲城市的投入为 (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为 (单位:万元).
(单位:万元).(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 定义在
定义在 上且满足下列两个条件:
上且满足下列两个条件:①对任意
 都有
都有 ;
;②当
 时,有
时,有 ,
,(1)求
 ,并证明函数
,并证明函数 在
在 上是奇函数;
上是奇函数;(2)验证函数
 是否满足这些条件;
是否满足这些条件;(3)若
 ,试求函数
,试求函数 的零点.
的零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
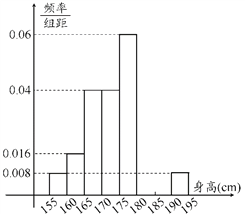
(2)求第六组、第七组的频率并补充完整频率分布直方图(如需增加刻度请在纵轴上标记出数据,并用直尺作图);(3)由直方图估计男生身高的中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,设倾斜角为
中,设倾斜角为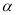 的直线
的直线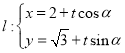 (
(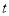 为参数)与曲线
为参数)与曲线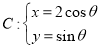 (
(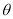 为参数)相交于不同的两点
为参数)相交于不同的两点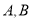 .
.(1)若
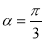 ,求线段
,求线段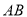 中点
中点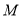 的坐标;
的坐标;(2)若
 ,其中
,其中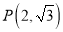 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
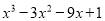 (x
(x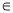 R),g(x)=2a-1
R),g(x)=2a-1(1)求函数f(x)的单调区间与极值.
(2)若f(x)≥g(x)对
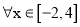 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3,
 ),点B的极坐标为(6,
),点B的极坐标为(6,  ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
相关试题

