【题目】已知 ![]() 且cos(
且cos( ![]() )=
)= ![]() ,sin
,sin ![]() 求cos(α+β)的值.
求cos(α+β)的值.
参考答案:
【答案】解:∵0<β< ![]() <α<π,cos(α﹣
<α<π,cos(α﹣ ![]() )=﹣
)=﹣ ![]() ,sin(
,sin( ![]() ﹣β)=
﹣β)= ![]() , ∴
, ∴ ![]() <α﹣
<α﹣ ![]() <π,0<
<π,0< ![]() ﹣β<
﹣β< ![]() ,
,
∴sin(α﹣ ![]() )=
)= 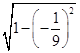 =
= ![]() ,cos(
,cos( ![]() ﹣β)=
﹣β)= 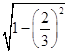 =
= ![]() ,
,
∴cos ![]() =cos[(α﹣
=cos[(α﹣ ![]() )﹣(
)﹣( ![]() ﹣β)]
﹣β)]
=cos(α﹣ ![]() )cos(
)cos( ![]() ﹣β)+sin(α﹣
﹣β)+sin(α﹣ ![]() )sin(
)sin( ![]() ﹣β)
﹣β)
=﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ,
,
则cos(α+β)=2cos2![]() ﹣1=﹣
﹣1=﹣ ![]()
【解析】根据α与β的范围求出α﹣ ![]() 与
与 ![]() ﹣β的范围,利用同角三角函数间的基本关系求出sin(α﹣
﹣β的范围,利用同角三角函数间的基本关系求出sin(α﹣ ![]() )与cos(
)与cos( ![]() ﹣β)的值,由cos[(α﹣
﹣β)的值,由cos[(α﹣ ![]() )﹣(
)﹣( ![]() ﹣β)],利用两角和与差的余弦函数公式化简,将各自的值代入求出cos
﹣β)],利用两角和与差的余弦函数公式化简,将各自的值代入求出cos ![]() 的值,所求式子利用二倍角的余弦函数公式化简,将求出cos
的值,所求式子利用二倍角的余弦函数公式化简,将求出cos ![]() 的值代入即可求出值.
的值代入即可求出值.
【考点精析】认真审题,首先需要了解两角和与差的余弦公式(两角和与差的余弦公式:![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

 经过点
经过点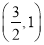 ,一个焦点是
,一个焦点是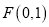 .
.(1)求椭圆
 的方程;
的方程;(2)若倾斜角为
 的直线
的直线 与椭圆
与椭圆 交于
交于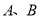 两点,且
两点,且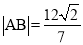 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆方程
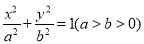 ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为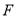 ,
, 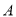 ,
, 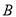 ,坐标原点为
,坐标原点为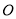 ,且线段
,且线段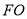 ,
, 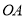 ,
, 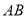 的长度成等差数列.
的长度成等差数列.(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点
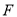 的一条直线
的一条直线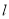 交椭圆于点
交椭圆于点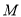 ,
, 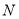 ,交
,交 轴于点
轴于点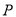 ,使得线段
,使得线段 被点
被点 ,
,  三等分,求直线
三等分,求直线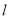 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】
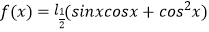 的单调递减区间为 .
的单调递减区间为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,
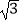 asinB+bcosA=c. (Ⅰ)求B;
asinB+bcosA=c. (Ⅰ)求B;
(Ⅱ)若a=2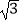 c,S△ABC=2
c,S△ABC=2 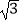 ,求b.
,求b. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知点
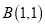 ,曲线
,曲线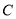 的参数方程为
的参数方程为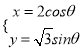 (
(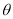 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以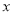 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点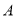 的极坐标为
的极坐标为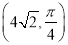 ,直线
,直线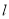 的极坐标方程为
的极坐标方程为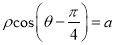 ,且
,且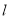 过点
过点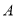 ;过点
;过点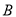 与直线
与直线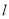 平行的直线为
平行的直线为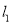 ,
, 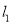 与曲线
与曲线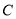 相交于两点
相交于两点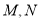 .
.(1)求曲线
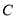 上的点到直线
上的点到直线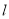 距离的最小值;
距离的最小值;(2)求
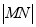 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为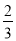 ,短轴长为
,短轴长为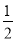 ,直线
,直线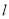 与椭圆
与椭圆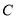 交于
交于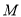 、
、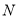 两点.
两点.(1)求椭圆
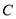 的方程;
的方程; (2)若直线
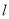 与圆
与圆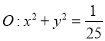 相切,探究
相切,探究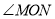 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
相关试题

