【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,一个焦点是
,一个焦点是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若倾斜角为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)利用题目所提供的条件布列关于a,b的方程组,解方程组得椭圆方程.
(2)根据直线的倾斜角为![]() ,设直线的方程为y=x+b联立椭圆方程,利用韦达定理以及弦长公式解得b值,从而得直线
,设直线的方程为y=x+b联立椭圆方程,利用韦达定理以及弦长公式解得b值,从而得直线![]() 的方程..
的方程..
试题解析:
(1)椭圆C: ![]() (a>b>0)经过点
(a>b>0)经过点![]() ,
,
则: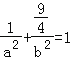 ①
①
椭圆的一个焦点是F(0,1).
则a2﹣b2=1 ②
由①②得:a2=4 b2=3
椭圆C的方程: ![]() ③
③
(2)根据题意可知:设直线l的方程为:y=x+b④
联立③④得: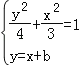
3(x+b)2+4x2=12
整理得:7x2+6bx+3b2﹣12=0
∴![]()
![]()
∵|AB|=![]() =
=![]() =
=![]()
解方程得:b=±2
直线l的方程为:y=x±2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
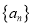 中,
中, 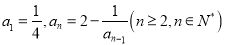 ,数列
,数列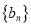 满足
满足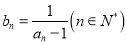 .
.(1)求证:数列
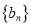 是等差数列,写出
是等差数列,写出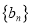 的通项公式;
的通项公式;(2)求数列
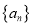 的通项公式及数列
的通项公式及数列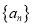 中的最大项与最小项.
中的最大项与最小项. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
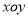 中,以坐标原点为极点,
中,以坐标原点为极点, 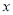 轴正半轴为极轴建立极坐标系,
轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:
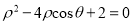 .
.(1)将极坐标方程化为直角坐标方程;
(2)若点
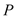
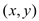 在该圆上,求
在该圆上,求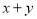 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
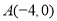 的动直线
的动直线 与抛物线
与抛物线 :
: 相交于
相交于 两点.当直线
两点.当直线 的斜率是
的斜率是 时,
时, .
.(1)求抛物线
 的方程;
的方程;(2)设线段
 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆方程
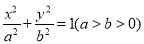 ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为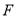 ,
, 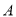 ,
, 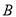 ,坐标原点为
,坐标原点为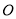 ,且线段
,且线段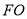 ,
, 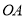 ,
, 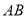 的长度成等差数列.
的长度成等差数列.(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点
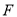 的一条直线
的一条直线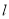 交椭圆于点
交椭圆于点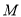 ,
, 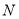 ,交
,交 轴于点
轴于点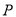 ,使得线段
,使得线段 被点
被点 ,
,  三等分,求直线
三等分,求直线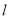 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】
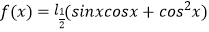 的单调递减区间为 .
的单调递减区间为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
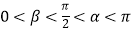 且cos(
且cos( 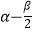 )=
)= 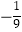 ,sin
,sin 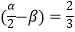 求cos(α+β)的值.
求cos(α+β)的值.
相关试题

