【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为![]() .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
参考答案:
【答案】(1)(x﹣2)2+4y2=4,  ,(t为参数);(2)
,(t为参数);(2)![]() .
.
【解析】试题分析:
(Ⅰ)极坐标方程化简直角坐标方程可得曲线C的直角坐标方程为(x﹣2)2+4y2=4,利用点的坐标和倾斜角可得直线的参数方程为 ,(t为参数);
,(t为参数);
(Ⅱ)利用题意求得伸缩变换之后的方程,然后利用弦长公式可得弦长为![]() .
.
试题解析:
(Ⅰ)∵曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,∴ρ2﹣4ρcosθ+3ρ2sin2θ=0,
∴曲线C的直角坐标方程为x2+y2﹣4x+3y2=0,整理,得(x﹣2)2+4y2=4,
∵直线l过点M(1,0),倾斜角为![]() ,
,
∴直线l的参数方程为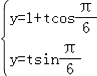 ,即
,即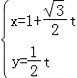 ,(t是参数).
,(t是参数).
(Ⅱ)∵曲线C经过伸缩变换![]() 后得到曲线C′,
后得到曲线C′,
∴曲线C′为:(x﹣2)2+y2=4,
把直线l的参数方程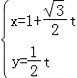 ,(t是参数)代入曲线C′:(x﹣2)2+y2=4,
,(t是参数)代入曲线C′:(x﹣2)2+y2=4,
得:![]() ,
,
设A,B对应的参数分别为t1,t2,则t1+t2=![]() ,t1t2=﹣3,
,t1t2=﹣3,
|MA|+|MB|=|t1|+|t2|=|t1﹣t2|=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是
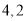 ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为 的正方形.
的正方形.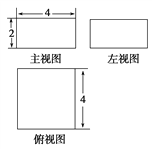
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点,若正方体的棱长为
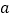 ,求这三个球的表面积.
,求这三个球的表面积.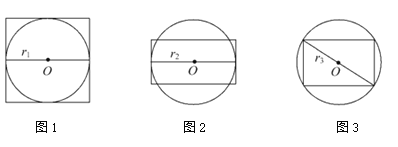
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
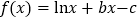 ,
, 在点
在点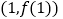 处的切线方程为
处的切线方程为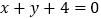 .
.(1)求
 的解析式;
的解析式;(2)求
 的单调区间;
的单调区间;(3)若函数
 在定义域内恒有
在定义域内恒有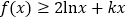 成立,求
成立,求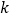 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
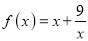 (
(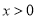 ).
).(1)判断函数
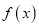 在
在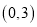 和
和 的单调性,并用定义证明
的单调性,并用定义证明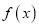 在
在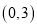 上的单调性;
上的单调性;(2)若函数
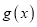 是定义域为
是定义域为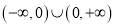 的偶函数,且
的偶函数,且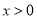 时,
时,  ,
,①当
 时,写出
时,写出 的表达式;
的表达式;②若函数
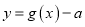 有四个零点,写出
有四个零点,写出 的取值范围(不需要说明理由).
的取值范围(不需要说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
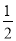 ﹣p
﹣p④回归直线一定过样本点的中心(
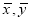 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
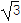 sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为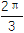 .
.(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
相关试题

