【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
参考答案:
【答案】C
【解析】解:y=loga(x+1)+1在[0,+∞)递减,则0<a<1,
函数f(x)在R上单调递减,则:
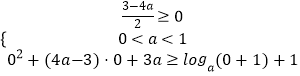 ;
;
解得, ![]() ;
;
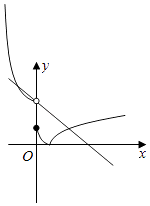
由图象可知,在[0,+∞)上,|f(x)|=2﹣x有且仅有一个解,
故在(﹣∞,0)上,|f(x)|=2﹣x同样有且仅有一个解,
当3a>2即a> ![]() 时,联立|x2+(4a﹣3)x+3a|=2﹣x,
时,联立|x2+(4a﹣3)x+3a|=2﹣x,
则△=(4a﹣2)2﹣4(3a﹣2)=0,
解得a= ![]() 或1(舍去),
或1(舍去),
当1≤3a≤2时,由图象可知,符合条件,
综上:a的取值范围为[ ![]() ,
, ![]() ]∪{
]∪{ ![]() },
},
所以答案是:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
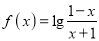 .
.(1)求不等式
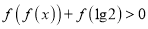 的解集;
的解集;(2)函数
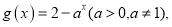 若存在
若存在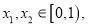 使得
使得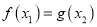 成立,求实数
成立,求实数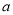 的取值范围;
的取值范围;(3)若函数
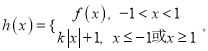 讨论函数
讨论函数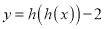 的零点个数(直接写出答案,不要求写出解题过程).
的零点个数(直接写出答案,不要求写出解题过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
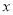 件,需另投入成本
件,需另投入成本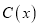 ,当年产量不足80件时,
,当年产量不足80件时, 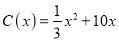 (万元),当年产量不少于80件时
(万元),当年产量不少于80件时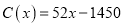 (万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.(1)写出年利润
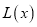 (万元)关于年产量
(万元)关于年产量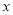 (件)的函数解析式;
(件)的函数解析式;(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2
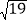 时,求直线l的方程.
时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 ,a∈R,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围为 .
,a∈R,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)(x∈R)是偶函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式;
(2)若不等式f(x)≥mx在1≤x≤2时都成立,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为
 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为ξ
0
1
2
3
p

x
y

(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
相关试题

