【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
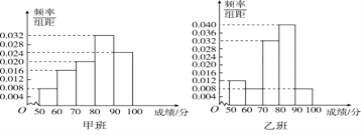
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】试题分析:(Ⅰ)由频率分布直方图分别求出甲乙班学生成绩优秀、不优秀人数,填入表格;(Ⅱ)根据计算公式,求出![]() ,得出结论。
,得出结论。
试题解析:(Ⅰ)由频率分布直方图可得,甲班成绩优秀、成绩不优秀的人数分别为12,38,乙班成绩优秀、成绩不优秀的人数分别为4,46.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | 12 | 4 | 16 |
成绩不优秀 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(Ⅱ)能判定,根据列联表中数据,计算![]()
由于4.762>3.841,所以在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
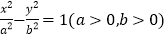 的实轴端点分别为
的实轴端点分别为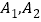 ,记双曲线的其中一个焦点为
,记双曲线的其中一个焦点为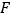 ,一个虚轴端点为
,一个虚轴端点为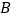 ,若在线段
,若在线段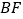 上(不含端点)有且仅有两个不同的点
上(不含端点)有且仅有两个不同的点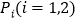 ,使得
,使得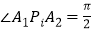 ,则双曲线的离心率
,则双曲线的离心率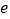 的取值范围是( )
的取值范围是( )A.
 B.
B. 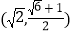 C.
C. 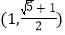 D.
D. 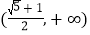
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份
2008
2009
2010
2011
2012
2013
2014
年份代号t
1
2
3
4
5
6
7
人均纯收入y
2.7
3.6
3.3
4.6
5.4
5.7
6.2
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
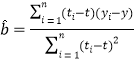 ,
,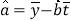
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2-2ax+2+b(a≠0)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-2mx在[2,4]上单调,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5
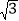 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
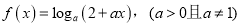
(1)设
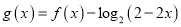 ,当
,当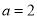 时,求函数
时,求函数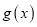 的定义域,判断并证明函数
的定义域,判断并证明函数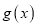 的奇偶性;
的奇偶性;(2)是否存在实数
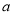 ,使得函数
,使得函数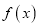 在
在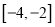 递减,并且最小值为1,若存在,求出
递减,并且最小值为1,若存在,求出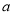 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
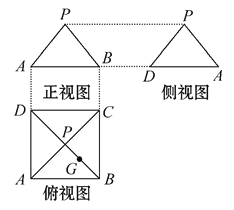
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
相关试题

