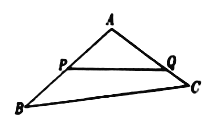
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,若
段围墙高2米,造价均为每平方米100元,若![]() ,求围墙总造价的取值范围.
,求围墙总造价的取值范围.
参考答案:
【答案】(1)![]() (米),
(米), ![]() (米2);(2)
(米2);(2)![]() .
.
【解析】试题分析:
(1)设![]() ,利用题意列出面积的表达式,最后利用均值不等式求解最值即可,注意讨论等号成立的条件和实际问题的定义域;
,利用题意列出面积的表达式,最后利用均值不等式求解最值即可,注意讨论等号成立的条件和实际问题的定义域;
(2)利用题意结合正弦定理求得围墙造价的函数解析式,利用三角形的性质求得![]() 的范围即可求得造价的取值范围.
的范围即可求得造价的取值范围.
试题解析:
设![]() (米),则
(米),则![]() ,所以
,所以![]() (米2)
(米2)
当且仅当![]() 时,取等号。即
时,取等号。即![]() (米),
(米), ![]() (米2)
(米2)
(2)由正弦定理![]() , 得
, 得![]()
故围墙总造价![]()
因为![]() , 所以
, 所以![]() ,
, ![]()
所以围墙总造价的取值范围为![]() (元)
(元)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取
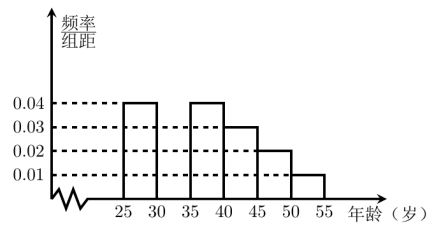
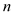 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:组数
分组
低碳族的人数
占本组的频率
第一组
[25,30)
120
0.6
第二组
[30,35)
195
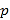
第三组
[35,40)
100
0.5
第四组
[40,45)

0.4
第五组
[45,50)
30
0.3
第六组
[50,55]
15
0.3
(1)补全频率分布直方图并求
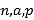 的值;
的值;(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在菱形
 中,
中,  ,
,  为
为 的中点,现将四边形
的中点,现将四边形 沿
沿 折起至
折起至 ,如图2.
,如图2.
(1)求证:
 面
面 ;
;(2)若二面角
 的大小为
的大小为 ,求平面
,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
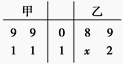
查看答案和解析>>【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率等于
 .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x|x﹣a|(其中a∈R).
(1)当a=1时,求函数f(x)的值域;
(2)若y=f(x)在[0,2]上的最小值为﹣1,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
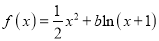 (
(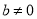 ).
).(1)若函数
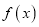 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数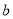 的取值范围;
的取值范围;(2)求函数
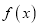 的极值点;
的极值点;(3)令
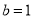 ,
, 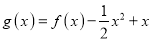 ,设
,设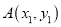 ,
, 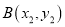 ,
,  是曲线
是曲线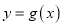 上相异三点,其中
上相异三点,其中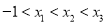 .求证:
.求证: 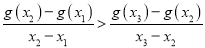 .
.
相关试题

