【题目】已知函数f(x)=x2﹣2x|x﹣a|(其中a∈R).
(1)当a=1时,求函数f(x)的值域;
(2)若y=f(x)在[0,2]上的最小值为﹣1,求a的值.
参考答案:
【答案】
(1)解:当a=1时,f(x)=x2﹣2x|x﹣1|
= 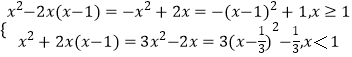 ,
,
当x≥1时,f(x)递减,可得f(x)∈(﹣∞,1];
当x<1时,f(x)∈[﹣ ![]() ,+∞).
,+∞).
则函数f(x)的值域(﹣∞,+∞)
(2)解: 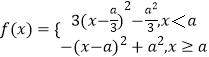 ,
,
①当a≤0时,f(x)在(0,2)上为减函数,
故 ![]() ,
,
可得 ![]() ,不符.
,不符.
②当a>0时,可知f(x)在 ![]() 上为减函数,在
上为减函数,在 ![]() 上为增函数.
上为增函数.
(i)当 ![]() 时,
时, ![]() ,得
,得 ![]() ,不符;
,不符;
(ii)当 ![]() 时,
时, ![]() ,得
,得 ![]() ,不符;
,不符;
(iii)当a≤2时, ![]() 或
或 ![]()
得 ![]() 或
或 ![]() ,符合.
,符合.
综上所述 ![]() 或
或 ![]()
【解析】(1)求出a=1时,f(x)的解析式,讨论x的范围,求得二次函数的值域,进而得到所求;(2)求出f(x)的分段函数式,讨论a的范围,结合二次函数的单调性,可得最小值,进而得到a的值.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
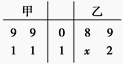
查看答案和解析>>【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生态园将一块三角形地
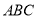 的一角
的一角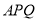 开辟为水果园,已知角
开辟为水果园,已知角 为
为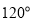 ,
,  的长度均大于200米,现在边界
的长度均大于200米,现在边界 处建围墙,在
处建围墙,在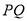 处围竹篱笆.
处围竹篱笆.(1)若围墙
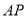 、
、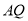 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块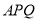 面积最大?
面积最大?(2)已知竹篱笆长为
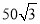 米,
米, 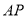 段围墙高1米,
段围墙高1米,  段围墙高2米,造价均为每平方米100元,若
段围墙高2米,造价均为每平方米100元,若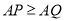 ,求围墙总造价的取值范围.
,求围墙总造价的取值范围.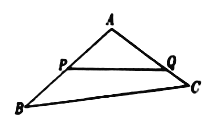
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率等于
 .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
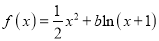 (
(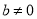 ).
).(1)若函数
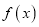 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数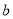 的取值范围;
的取值范围;(2)求函数
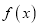 的极值点;
的极值点;(3)令
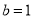 ,
, 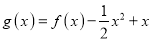 ,设
,设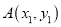 ,
, 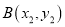 ,
,  是曲线
是曲线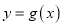 上相异三点,其中
上相异三点,其中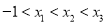 .求证:
.求证: 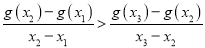 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】经销商经销某种农产品,在一个销售季度内,每售出
 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每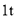 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了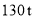 该农产品.以
该农产品.以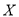 (
(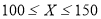 )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, 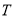 (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.(Ⅰ)将
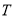 表示为
表示为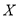 的函数;
的函数;(Ⅱ)根据直方图估计利润
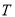 不少于57000元的概率.
不少于57000元的概率.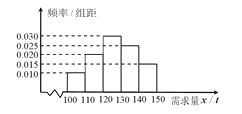
-
科目: 来源: 题型:
查看答案和解析>>【题目】
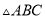 是等边三角形,边长为4,
是等边三角形,边长为4, 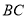 边的中点为
边的中点为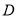 ,椭圆
,椭圆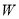 以
以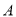 ,
,  为左、右两焦点,且经过
为左、右两焦点,且经过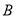 、
、 两点。
两点。(1)求该椭圆的标准方程;
(2)过点
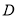 且
且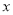 轴不垂直的直线
轴不垂直的直线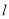 交椭圆于
交椭圆于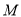 ,
, 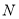 两点,求证:直线
两点,求证:直线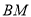 与
与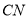 的交点在一条定直线上.
的交点在一条定直线上.
相关试题

