【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:当![]() 时,
时, ![]() ;
;
(Ⅲ)确定实数![]() 的值,使得存在
的值,使得存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
参考答案:
【答案】(1) 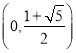 (2)见解析(3)
(2)见解析(3)![]()
【解析】【试题分析】(I)先求函数的定义域,然后求导令导数大于零即可求得函数的递增区间.(II)构造函数![]() ,利用导数求得函数在
,利用导数求得函数在![]() 时函数值小于零,由此证得不等式成立.(III)由(II)可知
时函数值小于零,由此证得不等式成立.(III)由(II)可知![]() 时不存在.当
时不存在.当![]() 时,有
时,有![]() ,则
,则![]() ,故也不存在.当
,故也不存在.当![]() 时,构造函数
时,构造函数![]() ,利用导致证得不等式成立,故
,利用导致证得不等式成立,故![]() .
.
【试题解析】
(Ⅰ)![]() ,
, ![]() .
.
由![]() 得
得![]() 解得
解得![]() .
.
故![]() 的单调递增区间是
的单调递增区间是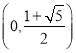 .
.
(Ⅱ)令![]() ,
, ![]() .
.
则有![]() .
.
当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
故当![]() 时,
时, ![]() ,即当
,即当![]() 时,
时, ![]() .
.
(Ⅲ)由(Ⅱ)知,当![]() 时,不存在
时,不存在![]() 满足题意.
满足题意.
当![]() 时,对于
时,对于![]() ,有
,有![]() ,则
,则![]() ,从而不存在
,从而不存在![]() 满足题意.
满足题意.
当![]() 时,令
时,令![]() ,
, ![]() ,
,
则有![]()
![]() .
.
由![]() 得,
得, ![]() .
.
解得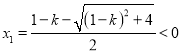 ,
, 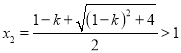 .
.
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 内单调递增.
内单调递增.
从而当![]() 时,
时, ![]() ,即
,即![]() ,
,
综上, ![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
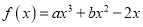 ,且
,且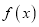 在
在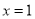 和
和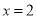 处取得极值.
处取得极值.(Ⅰ)求函数
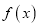 的解析式;
的解析式;(Ⅱ)设函数
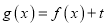 ,是否存在实数
,是否存在实数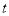 ,使得曲线
,使得曲线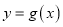 与
与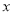 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出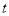 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点
 ,
,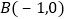 ,圆C的方程为
,圆C的方程为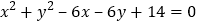 ,点P为圆上的动点.
,点P为圆上的动点.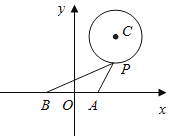
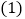 求过点A的圆C的切线方程.
求过点A的圆C的切线方程. 求
求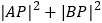 的最大值及此时对应的点P的坐标.
的最大值及此时对应的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ,证明:
,证明:  +
+  +…+
+…+  <
<  Sn+1(n∈N*).
Sn+1(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两俱乐部举行乒乓球团体对抗赛.双方约定:
①比赛采取五场三胜制(先赢三场的队伍获得胜利.比赛结束)
②双方各派出三名队员.前三场每位队员各比赛﹣场
已知甲俱乐部派出队员A1、A2 . A3 , 其中A3只参加第三场比赛.另外两名队员A1、A2比赛场次未定:乙俱乐部派出队员B1、B2 . B3 , 其中B1参加第一场与第五场比赛.B2参加第二场与第四场比赛.B3只参加第三场比赛
根据以往的比赛情况.甲俱乐部三名队员对阵乙俱乐部三名队员获胜的概率如表:A1
A2
A3
B1



B2



B3



(1)若甲俱乐部计划以3:0取胜.则应如何安排A1、A2两名队员的出场顺序.使得取胜的概率最大?
(2)若A1参加第一场与第四场比赛,A2参加第二场与第五场比赛,各队员每场比赛的结果互不影响,设本次团体对抗赛比赛的场数为随机变量X,求X的分布列及数学期望E(X) -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 的离心率是
的离心率是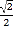 ,过点
,过点 的动直线
的动直线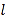 与椭圆相交于
与椭圆相交于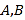 两点,当直线
两点,当直线 与
与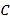 轴平行时,直线
轴平行时,直线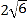 被椭圆
被椭圆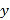 截得的线段长为
截得的线段长为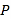 .
.(Ⅰ)求椭圆
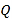 的方程;
的方程;(Ⅱ)在
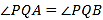 轴上是否存在异于点
轴上是否存在异于点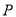 的定点
的定点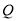 ,使得直线
,使得直线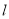 变化时,总有
变化时,总有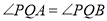 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C1:
 +
+  =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为  ,其右焦点到直线2ax+by﹣
,其右焦点到直线2ax+by﹣  =0的距离为
=0的距离为  .
.
(1)求椭圆C1的方程;
(2)过点P(0,﹣ )的直线l交椭圆C1于A,B两点.
)的直线l交椭圆C1于A,B两点.
①证明:线段AB的中点G恒在椭圆C2: +
+  =1的内部;
=1的内部;
②判断以AB为直径的圆是否恒过定点?若是,求出该定点的坐标;若不是,请说明理由.
相关试题

