【题目】设点O为坐标原点,椭圆E:![]() (a≥b>0)的右顶点为A,上顶点为B,过点O且斜率为
(a≥b>0)的右顶点为A,上顶点为B,过点O且斜率为![]() 的直线与直线AB相交M,且
的直线与直线AB相交M,且![]() .
.
(Ⅰ)求椭圆E的离心率e;
(Ⅱ)PQ是圆C:(x-2)2+(y-1)2=5的一条直径,若椭圆E经过P,Q两点,求椭圆E的方程.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)利用OM的斜率为![]() ,布列方程,解出离心率;(2)利用弦长公式,结合维达定理,布列方程,结合上一问的离心率,易得椭圆方程.
,布列方程,解出离心率;(2)利用弦长公式,结合维达定理,布列方程,结合上一问的离心率,易得椭圆方程.
试题解析:
(Ⅰ)∵A(a,0),B(0,b),![]() ,所以M(
,所以M(![]() ,
,![]() ).
).
∴![]() ,解得a=2b,
,解得a=2b,
于是![]() ,∴椭圆E的离心率e为
,∴椭圆E的离心率e为![]() .
.
(Ⅱ)由(Ⅰ)知a=2b,∴椭圆E的方程为![]() 即x2+4y2=4b2(1)
即x2+4y2=4b2(1)
依题意,圆心C(2,1)是线段PQ的中点,且![]() .
.
由对称性可知,PQ与x轴不垂直,设其直线方程为y=k(x-2)+1,代入(1)得:
(1+4k2)x2-8k(2k-1)x+4(2k-1)2-4b2=0
设P(x1,y1),Q(x2,y2),则![]() ,
,![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() .
.
从而x1x2=8-2b2.于是
![]() .
.
解得:b2=4,a2=16,∴椭圆E的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
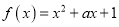
(Ⅰ)设
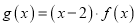 ,若
,若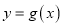 的图象与x轴恰有两个不同的交点,求实数a的取值集合.
的图象与x轴恰有两个不同的交点,求实数a的取值集合.(Ⅱ)求函数
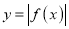 在区间
在区间 上的最大值.
上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如右表.
组
号
年龄
访谈
人数
愿意
使用
1
[18,28)
4
4
2
[28,38)
9
9
3
[38,48)
16
15
4
[48,58)
15
12
5
[58,68)
6
2
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数
年龄低于48岁的人数
合计
愿意使用的人数
不愿意使用的人数
合计
参考公式:
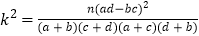 ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.P(k2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 在区间
在区间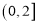 上单调递增;
上单调递增;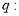 函数
函数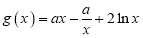 在其定义域上存在极值.
在其定义域上存在极值.(1)若
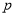 为真命题,求实数
为真命题,求实数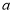 的取值范围;
的取值范围;(2)如果“
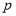 或
或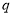 ”为真命题,“
”为真命题,“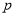 且
且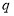 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x
[11,13)
[13,15)
[15,17)
[17,19)
[19,21)
[21,23)
频数
2
12
34
38
10
4
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点,一个焦点为
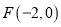 ,且长轴与短轴长的比是
,且长轴与短轴长的比是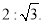
(1)求椭圆C的方程;
(2)设点
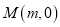 在 椭圆C的长轴上,点P是椭圆上任意一点,当
在 椭圆C的长轴上,点P是椭圆上任意一点,当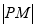 最小时,点P恰好落在椭圆的右顶点上,求实数
最小时,点P恰好落在椭圆的右顶点上,求实数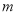 的取值范围.
的取值范围.
相关试题

