【题目】
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线方程为
l:y=3x+1,且当x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
参考答案:
【答案】(1) a=2,b=-4, c=5 (2) 最大值为13,最小值为![]()
【解析】试题分析:(1)对函数进行求导,当x=1时,切线l的斜率为3,可得2a+b=0,当x=![]() 时,y=f(x)有极值,则f′
时,y=f(x)有极值,则f′![]() =0,联立得出a,b,c的值(2) 由(1)可得f(x)=x3+2x2-4x+5, f′(x)=3x2+4x-4. 令f′(x)=0,解得x1=-2,x2=
=0,联立得出a,b,c的值(2) 由(1)可得f(x)=x3+2x2-4x+5, f′(x)=3x2+4x-4. 令f′(x)=0,解得x1=-2,x2=![]() ,研究单调性得出最值.
,研究单调性得出最值.
试题解析:
(1)由f(x)=x3+ax2+bx+c,
得f′(x)=3x2+2ax+b.
当x=1时,切线l的斜率为3,可得2a+b=0,①
当x=![]() 时,y=f(x)有极值,则f′
时,y=f(x)有极值,则f′![]() =0,可得4a+3b+4=0,②
=0,可得4a+3b+4=0,②
由①②,解得a=2,b=-4.
由于切点的横坐标为1,所以f(1)=4. 所以1+a+b+c=4,得c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5, f′(x)=3x2+4x-4.
令f′(x)=0,解得x1=-2,x2=![]() .
.
当x变化时,f′(x),f(x)的取值及变化情况如下表所示:
x | -3 | (-3,-2) | -2 |
|
|
| 1 |
f′(x) | + | 0 | - | 0 | + | ||
f(x) | 8 | 13 |
| 4 |
所以y=f(x)在[-3,1]上的最大值为13,最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f(
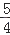 ),c=﹣f(
),c=﹣f(  )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+
 +alnx.
+alnx.(Ⅰ)若f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅱ)设f(x)的导数f’(x )的图象为曲线C ,曲线C 上的不同两点A (x1, y1) ,B (x2,y 2) 所在直线的斜率为k ,求证:当a≤4时,|k|>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
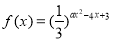 ,
,(Ⅰ)若
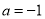 ,求
,求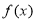 的单调区间;(Ⅱ)若
的单调区间;(Ⅱ)若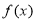 有最大值3,求
有最大值3,求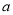 的值;(Ⅲ)若
的值;(Ⅲ)若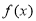 的值域是
的值域是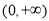 ,求
,求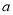 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)的定义域,值域分别为A,B,且A∩B是单元集,下列命题中:
①若A∩B={a},则f(a)=a;
②若B不是单元集,则满足f[f(x)]=f(x)的x值可能不存在;
③若f(x)具有奇偶性,则f(x)可能为偶函数;
④若f(x)不是常数函数,则f(x)不可能为周期函数.
正确命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】海南中学对高二学生进行心理障碍测试得到如下列联表:
焦虑
说谎
懒惰
总计
女生
5
10
15
30
男生
20
10
50
80
总计
25
20
65
110
试说明在这三种心理障碍中哪一种与性别关系最大?
参考数据:K2=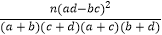
P(K2≥k)
0.5
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.535
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集
相关试题

