【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)设函数![]() ,
,![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
,![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析(2)1(3)![]()
【解析】试题分析:
(1) 当![]() 时,
时,![]() ,可得函数
,可得函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间为
,单调减区间为![]() ;
;
(2) ![]() ,令
,令![]() 得
得![]() ,
,
函数![]() 在
在![]() 上单调减;函数
上单调减;函数![]() 在
在![]() 上单调增.
上单调增.
所以![]() .分类讨论:
.分类讨论:
①当![]() 时,
时,![]() ;
;
②当![]() 时,解得
时,解得![]() (舍).
(舍).
综上所述,![]() 的值为1.
的值为1.
(3)由题意可知函数![]() 在
在![]() 上单调增,故
上单调增,故![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
构造函数:设![]() ,设
,设![]() ,结合函数的性质可得,
,结合函数的性质可得,![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
解:(1) 当![]() 时,
时,![]() ,
,![]() .
.
因为![]() 在
在![]() 上单调增,且
上单调增,且![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调增区间是
的单调增区间是![]() .
.
(2)![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调减;
上单调减;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调增.
上单调增.
所以![]() .
.
①当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值![]()
![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),所以
(舍),所以![]() ;
;
②当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值![]() ,解得
,解得![]() (舍).
(舍).
综上所述,![]() 的值为1.
的值为1.
(3)由题意知,![]() ,
,![]() .
.
考虑函数![]() ,因为
,因为![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调增,故
上单调增,故![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
设![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]() .
.
设![]() ,
,
则![]()
![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调增,所以
上单调增,所以![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列
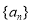 满足
满足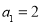 ,
,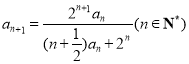 .
.(1)设
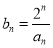 ,求数列
,求数列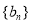 的通项公式;
的通项公式;(2)设
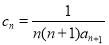 ,求数列
,求数列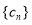 的前n项和为
的前n项和为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了
 ,
, 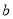 ,
, 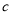 ,
, 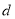 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是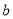 ,3号门里是
,3号门里是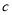 ;乙同学说:2号门里是
;乙同学说:2号门里是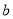 ,3号门里是
,3号门里是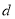 ;丙同学说:4号门里是
;丙同学说:4号门里是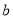 ,2号门里是
,2号门里是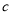 ;丁同学说:4号门里是
;丁同学说:4号门里是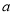 ,3号门里是
,3号门里是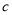 .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )A.
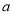 B.
B. 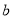 C.
C. 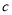 D.
D. 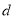
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列{an}的前n项和为Sn , 且an和Sn满足:4Sn=(an+1)2(n=1,2,3…),
(1)求{an}的通项公式;
(2)设bn= ,求{bn}的前n项和Tn .
,求{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x=3﹣
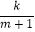 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆
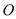 的圆心与矩形
的圆心与矩形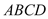 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(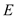 为上切点),与左右两边相交(
为上切点),与左右两边相交(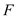 ,
, 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1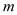 ,且
,且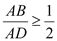 ,设
,设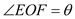 ,透光区域的面积为
,透光区域的面积为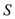 .
.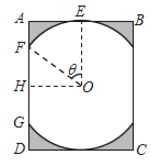
(1)求
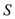 关于
关于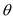 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边
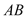 的长度.
的长度.
相关试题

