【题目】从装有![]() 个不同小球的口袋中取出
个不同小球的口袋中取出![]() 个小球(
个小球(![]() ),共有
),共有![]() 种取法。在这
种取法。在这![]() 种取法中,可以视作分为两类:第一类是某指定的小球未被取到,共有
种取法中,可以视作分为两类:第一类是某指定的小球未被取到,共有![]() 种取法;第二类是某指定的小球被取到,共有
种取法;第二类是某指定的小球被取到,共有![]() 种取法。显然
种取法。显然![]() ,即有等式:
,即有等式:![]() 成立。试根据上述想法,下面式子
成立。试根据上述想法,下面式子![]() (其中
(其中![]() )应等于 ( )
)应等于 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】分析:从装有![]() 个不同小球的口袋中取出
个不同小球的口袋中取出![]() 个小球(
个小球(![]() ),共有
),共有![]() 种取法。在这
种取法。在这![]() 种取法中,可以视作分为两类:第一类是某指定的小球未被取到,第二类是某指定的小球被取到,即有等式:
种取法中,可以视作分为两类:第一类是某指定的小球未被取到,第二类是某指定的小球被取到,即有等式:![]() 成立,题中的式子表示的是从装有
成立,题中的式子表示的是从装有![]() 个球中取出
个球中取出![]() 个球的不同取法数
个球的不同取法数![]() ,从而得到选项.
,从而得到选项.
详解:在![]() 中,从第一项到最后一项分别表示:
中,从第一项到最后一项分别表示:
从装有![]() 个白球,
个白球,![]() 个黑球的袋子里,取出
个黑球的袋子里,取出![]() 个球的所有情况取法总数的和,故答案为:从装有
个球的所有情况取法总数的和,故答案为:从装有![]() 个球中取出
个球中取出![]() 个球的不同取法数
个球的不同取法数![]() ,故选A.
,故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知偶函数
 满足:当
满足:当 时,
时, ,
, ,当
,当 时,
时, .
.(
 )求当
)求当 时,
时, 的表达式.
的表达式.(
 )若直线
)若直线 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围.
的取值范围.(
 )试讨论当实数
)试讨论当实数 ,
, 满足什么条件时,函数
满足什么条件时,函数 有
有 个零点且这
个零点且这 个零点从小到大依次成等差数列.
个零点从小到大依次成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
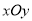 中,过椭圆
中,过椭圆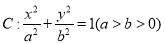 右焦点
右焦点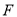 的直线
的直线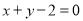 交椭圆
交椭圆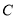 于
于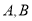 两点 ,
两点 , 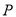 为
为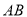 的中点,且
的中点,且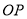 的斜率为
的斜率为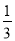 .
. (1)求椭圆
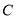 的标准方程;
的标准方程;(2)设过点
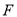 的直线
的直线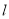 (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆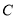 交于
交于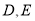 两点,问:在
两点,问:在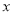 轴上是否存在定点
轴上是否存在定点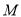 ,使得
,使得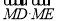 为定值?若存在,求出点
为定值?若存在,求出点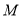 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:(1)异面直线是指空间两条既不平行也不相交的直线;(2)若直线
 上有两点到平面
上有两点到平面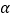 的距离相等,则
的距离相等,则 ;(3)若直线
;(3)若直线 与平面
与平面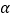 内无穷多条直线都垂直,则
内无穷多条直线都垂直,则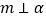 ;(4)两条异面直线中的一条垂直于平面
;(4)两条异面直线中的一条垂直于平面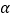 ,则另一条必定不垂直于平面
,则另一条必定不垂直于平面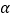 .其中正确命题的个数是 ( )
.其中正确命题的个数是 ( )A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
 在
在 处有极值
处有极值 ,求
,求 的值;
的值;(2)若对于任意的
 在
在 上单调递增,求
上单调递增,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
 的前
的前 项和为
项和为 ,若数列
,若数列 的各项按如下规律排列;
的各项按如下规律排列; 有如下运算结论:①
有如下运算结论:① ;②数列
;②数列 是等比数列;③数列
是等比数列;③数列 的前
的前 项和为
项和为 ;④若存在正整数
;④若存在正整数 ,使得
,使得 ,则
,则 ,
,其中正确的结论是________(将你认为正确的结论序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=aln(x2+1)+bx存在两个极值点x1 , x2 .
(1)求证:|x1+x2|>2;
(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,试求λ的取值范围.
相关试题

