【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点 ,
两点 , ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆![]() 交于
交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)当点
(2)当点![]() 的坐标为
的坐标为![]() 时,
时, ![]() 为定值.
为定值.
【解析】试题分析:
(1)利用题意结合几何关系可求得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]()
(2)设出直线方程,与椭圆方程联立,整理可得当点![]() 的坐标为
的坐标为![]() 时,
时, ![]() 为定值.
为定值.
试题解析:
解:(1) 设![]() ,则
,则![]() ,两式相减得,
,两式相减得,
![]() ,又
,又![]() ,
, ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() ,所以
,所以![]() ,即
,即![]() ,所以可以解得
,所以可以解得![]() ,即
,即![]() ,即
,即![]() ,又因为
,又因为![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2) 设直线![]() 的方程为
的方程为![]() ,代入椭圆
,代入椭圆![]() 的方程为
的方程为![]() ,得
,得![]() ,设
,设![]() ,则
,则![]() .
.
![]() ,根据题意,假设
,根据题意,假设![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值,则有
为定值,则有![]()
![]()
![]() ,要使上式为定值,即与
,要使上式为定值,即与![]() 无关,则应
无关,则应![]() ,即
,即![]() ,故当点
,故当点![]() 的坐标为
的坐标为![]() 时,
时, ![]() 为定值.
为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
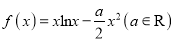 .
.(1)若
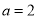 ,求曲线
,求曲线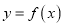 在点
在点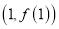 处的切线方程;
处的切线方程;(2)若
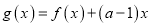 在
在 处取得极小值,求实数
处取得极小值,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD中,
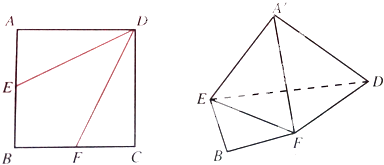
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= BC时,求三棱锥A′﹣EFD的体积.
BC时,求三棱锥A′﹣EFD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】求满足下列条件的椭圆方程:
(1)长轴在x轴上,长轴长等于12,离心率等于 ;
;
(2)椭圆经过点(﹣6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=3x2+bx+c,不等式f(x)>0的解集为(﹣∞,﹣2)∪(0,+∞).
(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+mx﹣2在(2,+∞)上单调递增,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中,已知a1=1,
 ,
,
(1)求证数列{ }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)若对一切n∈N* , 等式a1b1+a2b2+a3b3+…+anbn=2n恒成立,求数列{bn}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,P、Q分别为边AB、DA上的点,当△APQ的周长为2时,求∠PCQ的大小.
相关试题

