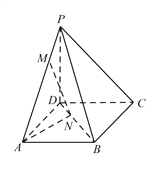
【题目】如图,四棱锥 ![]() 底面为正方形,已知
底面为正方形,已知 ![]() ,
,![]() ,点
,点 ![]() 为线段
为线段 ![]() 上任意一点(不含端点),点
上任意一点(不含端点),点 ![]() 在线段
在线段 ![]() 上,且
上,且 ![]() .
.
(1)求证:![]() ;
;
(2)若 ![]() 为线段
为线段 ![]() 中点,求直线
中点,求直线 ![]() 与平面
与平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)延长![]() ,交
,交![]() 于点
于点![]() ,由相似三角形的性质可知
,由相似三角形的性质可知 ![]() ,从而得
,从而得![]() ,利用线面平行的判定定理可得直线
,利用线面平行的判定定理可得直线![]() 平面
平面![]() ;(2)由于
;(2)由于 ![]() ,
,![]() ,
,![]() 两两垂直,所以,以
两两垂直,所以,以![]() 为
为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设 ![]() ,求出相关点的坐标及直线
,求出相关点的坐标及直线 ![]() 的方向向量,根据向量垂直数量积为零列方程组,求出平面
的方向向量,根据向量垂直数量积为零列方程组,求出平面 ![]() 的一个法向量,空间向量夹角余弦公式,可求解
的一个法向量,空间向量夹角余弦公式,可求解![]() 与平面
与平面 ![]() 夹角的正弦值,进而可求余弦值.
夹角的正弦值,进而可求余弦值.
试题解析:(1) 延长 ![]() ,交
,交 ![]() 于点
于点 ![]() ,连接
,连接 ![]() ,
,
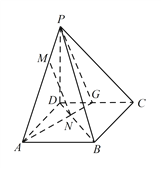
由相似知 ![]() ,可得:
,可得:![]() ,
,
![]() ,
,![]() ,
,
则 ![]() .
.
(2) 由于 ![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以 ![]() ,
,![]() ,
,![]() 为
为 ![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
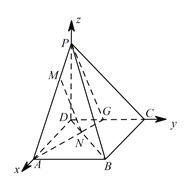
设 ![]() ,则
,则 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则 ![]() ,平面
,平面 ![]() 的法向量为
的法向量为 ![]() ,
,
设向量 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,则
,则 ![]() ,
,
则 ![]() 与平面
与平面 ![]() 夹角的余弦值为
夹角的余弦值为 ![]() .
.
【方法点晴】本题主要考查线面平行的判定定理以及利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 恒成立;命题
恒成立;命题 方程
方程 表示双曲线.
表示双曲线.(1)若命题
 为真命题,求实数
为真命题,求实数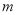 的取值范围;
的取值范围;(2)若命题“
 ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三棱柱
 的底面边长为2,
的底面边长为2,  是侧棱
是侧棱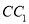 的中点.
的中点.
(1)证明:平面
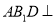 平面
平面 ;
;(2)若平面
 与平面
与平面 所成锐角的大小为
所成锐角的大小为 ,求四棱锥
,求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
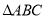 的两个顶点
的两个顶点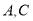 的坐标分别为
的坐标分别为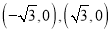 ,三个内角
,三个内角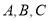 满足
满足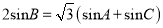 .
.(1)若顶点
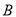 的轨迹为
的轨迹为 ,求曲线
,求曲线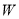 的方程;
的方程;(2)若点
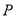 为曲线
为曲线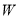 上的一点,过点
上的一点,过点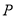 作曲线
作曲线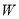 的切线交圆
的切线交圆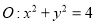 于不同的两点
于不同的两点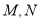 (其中
(其中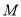 在
在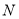 的右侧),求四边形
的右侧),求四边形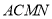 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线的焦点在x轴上,焦距为
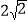 ,实轴长为2
,实轴长为2(1)求双曲线的标准方程与渐近线方程。
(2)若点
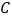 在该双曲线上运动,且
在该双曲线上运动,且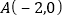 ,
,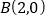 ,求以
,求以 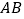 ,
,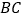 为相邻两边的平行四边形
为相邻两边的平行四边形 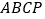 的顶点
的顶点 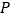 的轨迹.
的轨迹.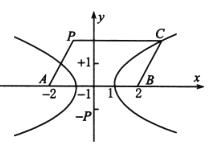
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 为椭圆
为椭圆  上任一点,
上任一点, ,
, 为椭圆的焦点,
为椭圆的焦点, ,离心率为
,离心率为  .
.(1)求椭圆的标准方程;
(2)直线
 经过点
经过点 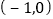 ,且与椭圆交于
,且与椭圆交于  ,
, 两点,若直线
两点,若直线  ,
, ,
, 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线  的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
相关试题

