【题目】已知双曲线的焦点在x轴上,焦距为![]() ,实轴长为2
,实轴长为2
(1)求双曲线的标准方程与渐近线方程。
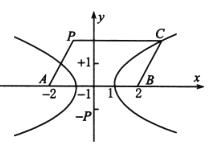
(2)若点 ![]() 在该双曲线上运动,且
在该双曲线上运动,且![]() ,
,![]() ,求以
,求以 ![]() ,
,![]() 为相邻两边的平行四边形
为相邻两边的平行四边形 ![]() 的顶点
的顶点 ![]() 的轨迹.
的轨迹.
参考答案:
【答案】(1)双曲线的方程为![]() ,渐近线方程为
,渐近线方程为![]() (2)
(2)![]()
【解析】试题分析:(1)根据焦距为![]() 可得
可得![]() ,由实轴长为
,由实轴长为![]() 可得
可得![]() ,从而可得
,从而可得![]() ,于是可得双曲线的标准方程与渐近线方程;(2)设点
,于是可得双曲线的标准方程与渐近线方程;(2)设点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]() ,则线段
,则线段 ![]() 的中点
的中点 ![]() 的坐标为
的坐标为  ,根据平行四边形的性质可得
,根据平行四边形的性质可得 所以
所以 ![]() ,代入双曲线方程得结果.
,代入双曲线方程得结果.
试题解析:(1)由题意可知![]() ,
,![]() ,所以
,所以![]() ,所以双曲线的方程为
,所以双曲线的方程为
![]() ,渐近线方程为
,渐近线方程为![]() ;
;
(2)设点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]() ,
,
则线段 ![]() 的中点
的中点 ![]() 的坐标为
的坐标为 
由平行四边形的性质,点 ![]() 也是线段
也是线段 ![]() 的中点,
的中点,
所以有 
因此 ![]() 可用
可用 ![]() ,
,![]() 表示,得
表示,得 ![]() ①
①
又由于 ![]() 在曲线
在曲线 ![]() 上,因此,
上,因此,![]() ②
②
①代入②,得 ![]() .
.
因为平行四边形不可能有两个以上的顶点在一条直线上,
所以动点 ![]() 的轨迹是除去两点
的轨迹是除去两点 ![]() ,
,![]() 的曲线
的曲线 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三棱柱
 的底面边长为2,
的底面边长为2,  是侧棱
是侧棱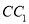 的中点.
的中点.
(1)证明:平面
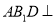 平面
平面 ;
;(2)若平面
 与平面
与平面 所成锐角的大小为
所成锐角的大小为 ,求四棱锥
,求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
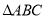 的两个顶点
的两个顶点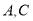 的坐标分别为
的坐标分别为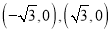 ,三个内角
,三个内角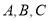 满足
满足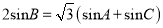 .
.(1)若顶点
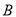 的轨迹为
的轨迹为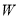 ,求曲线
,求曲线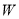 的方程;
的方程;(2)若点
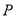 为曲线
为曲线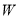 上的一点,过点
上的一点,过点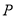 作曲线
作曲线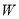 的切线交圆
的切线交圆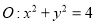 于不同的两点
于不同的两点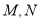 (其中
(其中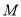 在
在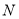 的右侧),求四边形
的右侧),求四边形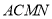 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 底面为正方形,已知
底面为正方形,已知  ,
,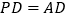 ,点
,点 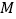 为线段
为线段 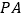 上任意一点(不含端点),点
上任意一点(不含端点),点 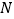 在线段
在线段 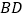 上,且
上,且 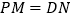 .
.(1)求证:
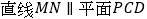 ;
;(2)若
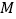 为线段
为线段 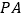 中点,求直线
中点,求直线  与平面
与平面 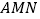 所成的角的余弦值.
所成的角的余弦值.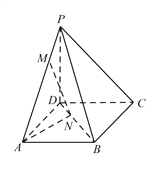
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 为椭圆
为椭圆  上任一点,
上任一点, ,
, 为椭圆的焦点,
为椭圆的焦点, ,离心率为
,离心率为  .
.(1)求椭圆的标准方程;
(2)直线
 经过点
经过点 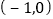 ,且与椭圆交于
,且与椭圆交于  ,
, 两点,若直线
两点,若直线  ,
, ,
, 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线  的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
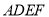 与梯形
与梯形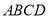 所在的平面互相垂直,
所在的平面互相垂直,  ,
,  ,点
,点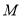 是线段
是线段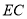 的中点.
的中点.
(1)求证:
 面
面 ;
;(2)求平面
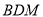 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
相关试题

