(本小题12分)设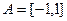 ,
,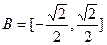 ,函数
,函数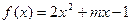 ,
,
(Ⅰ)设不等式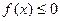 的解集为C,当
的解集为C,当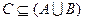 时,求实数
时,求实数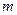 取值范围;
取值范围;
(Ⅱ)若对任意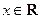 ,都有
,都有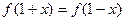 成立,试求
成立,试求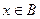 时,
时, 的值
的值 域;
域;
(Ⅲ)设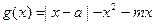
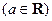 ,求
,求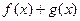 的最
的最 小值.
小值.
参考答案:
解:(1)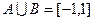 ,因为
,因为 ,二次函数
,二次函数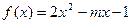 图像
图像
开口向上,且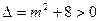 恒成立,故图像始终与
恒成立,故图像始终与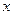 轴有两个交点,由题意,要使这两个
轴有两个交点,由题意,要使这两个
交点横坐标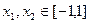 ,当且仅当:
,当且仅当: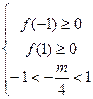 , 解得:
, 解得:

(2)对任意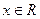 都有
都有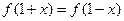 ,所以
,所以 图像关于直线
图像关于直线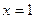 对称,
对称,
所以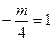 ,得
,得 .所以
.所以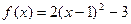 为
为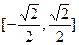 上减函数.
上减函数. 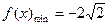 ;
;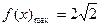 .故
.故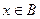 时,
时, 值域为
值域为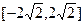 .
.
(3)令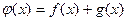 ,则
,则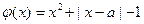
(i)当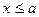 时,
时,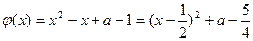 ,
,
当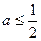 ,则函数
,则函数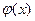 在
在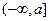 上单调递减,
上单调递减,
从而函数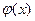 在
在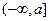 上的最小值为
上的最小值为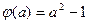 .
.
若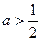 ,则函数
,则函数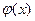 在
在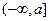 上
上 的最小值为
的最小值为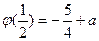 ,且
,且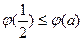 .
.
(ii) 当
当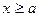 时,函数
时,函数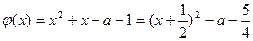
若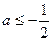 ,则函数
,则函数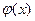 在
在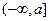 上的最小值为
上的最小值为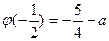 ,且
,且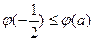
若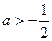 ,则函数
,则函数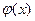 在
在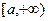 上单调递增,
上单调递增,
从而函数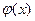 在
在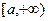 上的最小值为
上的最小值为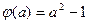 .
.
综上,当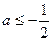 时,函数
时,函数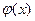 的最小值为
的最小值为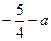
当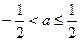 时,函数
时,函数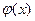 的最小值为
的最小值为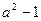
当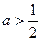 时,函数
时,函数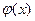 的最小值为
的最小值为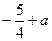
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>已知函数
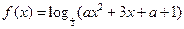
(1)当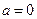 时,求函数
时,求函数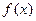 的定义域、值域及单调区间;
的定义域、值域及单调区间;
(2)对于 ,不等式
,不等式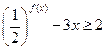 恒成立,求正实
恒成立,求正实 数
数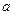 的取值范围.
的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>若定义在
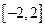 上的奇函数
上的奇函数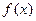 满足当
满足当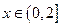 时,
时,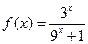 .
.
(1)求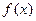 在
在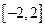 上的解析式;
上的解析式;
(2)判断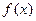 在
在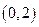 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当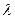 为何值时,关于方程
为何值时,关于方程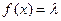 在
在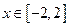 上有实数解?
上有实数解? -
科目: 来源: 题型:解答题
查看答案和解析>>已知
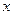 满足不等式
满足不等式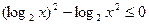 ,求函数
,求函数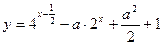 的最小值.
的最小值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分15分)某经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:

资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少? -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分13分)已知幂函数
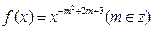 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数.
上是单调增函数.
(Ⅰ)求函数
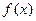 的解析式;
的解析式;
(Ⅱ)设函数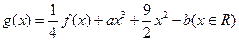 ,其中
,其中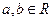 .若函数
.若函数 仅在
仅在
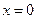 处有极值,求
处有极值,求 的取值范围.
的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分13
 分) 2010年11月在广州召开亚
分) 2010年11月在广州召开亚 运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平
运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平 均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均
均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均 销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
(1)写出y与x的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使该公司销售该纪念品的月平均利润最大.
相关试题

