若定义在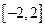 上的奇函数
上的奇函数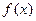 满足当
满足当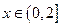 时,
时,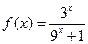 .
.
(1)求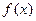 在
在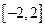 上的解析式;
上的解析式;
(2)判断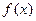 在
在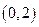 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当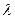 为何值时,关于方程
为何值时,关于方程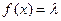 在
在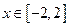 上有实数解?
上有实数解?
参考答案:
(1)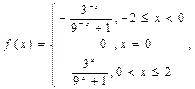 …………………………3分
…………………………3分
(2)任取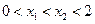
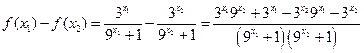
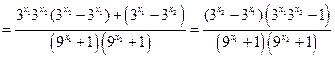 …3分
…3分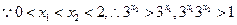
即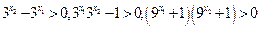 ,
,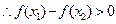 ……2分
……2分
因此: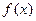 在
在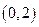 上单调递减。……………………………………1分
上单调递减。……………………………………1分
(3)方程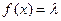 在
在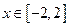 上有实数解即
上有实数解即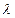 取函数
取函数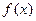 的值域内的任意值……………………………………………………………………2分
的值域内的任意值……………………………………………………………………2分
由(2)可知,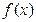 在
在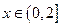 上是减函数,此时
上是减函数,此时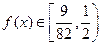 …1分
…1分
又
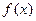 是
是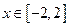 上的奇函数
上的奇函数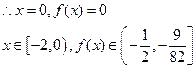
因此,函数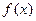 的值域为
的值域为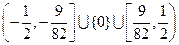 ………………2分
………………2分
因此,
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>求值:

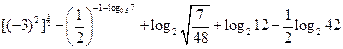
-
科目: 来源: 题型:解答题
查看答案和解析>>某化工厂生产的某种化工产品,当年产量在150吨至250吨之间时,其生产的总成本
 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式近似地表示为
(吨)之间的函数关系式近似地表示为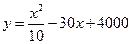 .问:(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
.问:(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
(2)年产量为多少吨时,每吨的平均成本最低? 并求出最低成本。
并求出最低成本。 -
科目: 来源: 题型:解答题
查看答案和解析>>已知函数
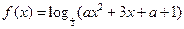
(1)当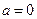 时,求函数
时,求函数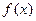 的定义域、值域及单调区间;
的定义域、值域及单调区间;
(2)对于 ,不等式
,不等式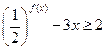 恒成立,求正实
恒成立,求正实 数
数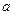 的取值范围.
的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>已知
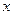 满足不等式
满足不等式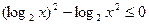 ,求函数
,求函数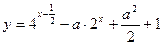 的最小值.
的最小值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题12分)设
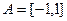 ,
,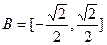 ,函数
,函数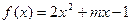 ,
,
(Ⅰ)设不等式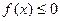 的解集为C,当
的解集为C,当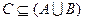 时,求实数
时,求实数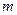 取值范围;
取值范围;
(Ⅱ)若对任意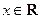 ,都有
,都有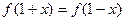 成立,试求
成立,试求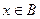 时,
时, 的值
的值 域;
域;
(Ⅲ)设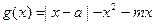
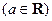 ,求
,求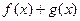 的最
的最 小值.
小值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分15分)某经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:

资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
相关试题

