【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量![]() ,
,![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数在![]() 上的最大值为3时,求
上的最大值为3时,求的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数,![]() 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间.
参考答案:
【答案】(Ⅰ)![]()
![]() .
.
【解析】试题分析:(1)把向量![]() 的坐标代入
的坐标代入![]()
![]() ,时
,时![]() ,最后对
,最后对![]()
(2)把![]()
![]()
![]()
试题解析:(Ⅰ)由已知得,![]()
![]()
![]() 时,
时,![]()
当![]()
![]()
![]()
![]()
当![]()
![]()
![]()
![]()
综上:函数![]()
![]() 上的最大值为3时,
上的最大值为3时,![]()
(Ⅱ)当![]()
![]() ,
,
由![]()
![]() 可知,
可知,![]()
![]() .
.
又由![]() ,可得,
,可得,
![]() ,
,
∵![]() ,
,
∴函数![]()
![]() 上的单调递减区间为
上的单调递减区间为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 与圆
与圆
 的公共点的轨迹为曲线
的公共点的轨迹为曲线 ,且曲线
,且曲线 与
与 轴的正半轴相交于点
轴的正半轴相交于点 .若曲线
.若曲线 上相异两点
上相异两点 满足直线
满足直线 的斜率之积为
的斜率之积为 .
.(1)求
 的方程;
的方程;(2)证明直线
 恒过定点,并求定点的坐标.
恒过定点,并求定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/
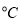
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是
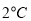 ,预测这天卖出的热饮杯数.
,预测这天卖出的热饮杯数. -
科目: 来源: 题型:
查看答案和解析>>【题目】【湖南省2017届高三长郡中学、衡阳八中等十三校重点中学第一次联考数学(理)】
已知函数
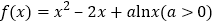 .
.(1)当
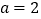 时,试求函数图像过点
时,试求函数图像过点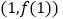 的切线方程;
的切线方程;(2)当
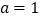 时,若关于
时,若关于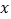 的方程
的方程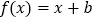 有唯一实数解,试求实数
有唯一实数解,试求实数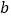 的取值范围;
的取值范围;(3)若函数
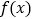 有两个极值点
有两个极值点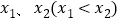 ,且不等式
,且不等式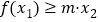 恒成立,试求实数
恒成立,试求实数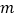 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】电视剧《人民的名义》中有一个低矮的接待上访服务窗口,假设群众办理业务所需的时间互相独立,且都是10分钟的整数倍,对以往群众办理业务所需的时间统计结果如下:
办理业务所需的时间(分)
10
20
30
40
50
频率
0.3
0.3
0.2
0.1
0.1
假设排队等待办理业务的群众不少于3人,从第一个群众开始办理业务时开始计时.
(Ⅰ)估计第三个群众恰好等待40分钟开始办理业务的概率;
(Ⅱ)
 表示至第20分钟末已办理完业务的群众人数,求
表示至第20分钟末已办理完业务的群众人数,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
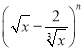 的展开式中,第5项的系数与第3项的系数之比是56:3.
的展开式中,第5项的系数与第3项的系数之比是56:3.(1)求展开式中的所有有理项;
(2)求展开式中系数绝对值最大的项.
(3)求
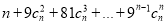 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,  轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .直线
.直线 过点
过点 .
.(1)若直线
 与曲线
与曲线 交于
交于 两点,求
两点,求 的值;
的值;(2)求曲线
 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
相关试题

