【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .直线
.直线![]() 过点
过点![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
参考答案:
【答案】(1)2;(2)16.
【解析】试题分析:(1)将直线l和椭圆C的转化为普通方程,左焦点F在直线l上,求解出直线1方程与椭圆C联立方程组,求解A,B坐标,利用两点之间的距离公式求解|FA||FB|的值.
(2)设椭圆在第一象限上一点P(acosθ,bsinθ),内接矩形周长为: ![]() ,即得答案.
,即得答案.
试题解析:
(1)已知曲线![]() 的标准方程为
的标准方程为 ![]() ,则其左焦点为
,则其左焦点为![]() ,则
,则![]() ,将直线
,将直线![]() 的参数方程
的参数方程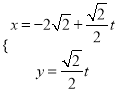 与曲线
与曲线![]() 的方程
的方程 ![]() 联立,得
联立,得![]() ,则
,则![]() .
.
(2)由曲线![]() 的方程为
的方程为 ![]() ,可设曲线
,可设曲线![]() 上的动点
上的动点![]() ,则以
,则以![]() 为顶点的内接矩形周长为
为顶点的内接矩形周长为![]() ,因此该内接矩形周长的最大值为
,因此该内接矩形周长的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量
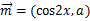 ,
,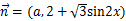 ,且函数
,且函数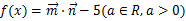 .
.(Ⅰ)当函数
在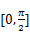 上的最大值为3时,求
上的最大值为3时,求的值;(Ⅱ)在(Ⅰ)的条件下,若对任意的
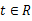 ,函数
,函数,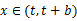 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】电视剧《人民的名义》中有一个低矮的接待上访服务窗口,假设群众办理业务所需的时间互相独立,且都是10分钟的整数倍,对以往群众办理业务所需的时间统计结果如下:
办理业务所需的时间(分)
10
20
30
40
50
频率
0.3
0.3
0.2
0.1
0.1
假设排队等待办理业务的群众不少于3人,从第一个群众开始办理业务时开始计时.
(Ⅰ)估计第三个群众恰好等待40分钟开始办理业务的概率;
(Ⅱ)
 表示至第20分钟末已办理完业务的群众人数,求
表示至第20分钟末已办理完业务的群众人数,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
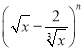 的展开式中,第5项的系数与第3项的系数之比是56:3.
的展开式中,第5项的系数与第3项的系数之比是56:3.(1)求展开式中的所有有理项;
(2)求展开式中系数绝对值最大的项.
(3)求
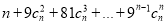 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
某公司经销某产品,第
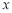 天
天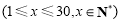 的销售价格为
的销售价格为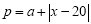 (
(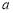 为常数)(元∕件),第
为常数)(元∕件),第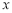 天的销售量为
天的销售量为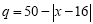 (件),且公司在第
(件),且公司在第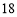 天该产品的销售收入为
天该产品的销售收入为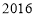 元.
元.(1)求该公司在第
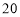 天该产品的销售收入是多少?
天该产品的销售收入是多少?(2)这
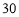 天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
天中该公司在哪一天该产品的销售收入最大?最大收入为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A. 264 B. 72 C. 266 D. 274
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
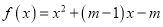 ,
, 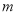 为实数.
为实数.(1)若关于
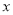 的不等式
的不等式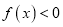 的解集为
的解集为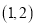 ,求实数
,求实数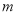 的值;
的值; (2)设
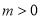 ,当
,当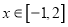 时,求函数
时,求函数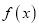 的最小值(用
的最小值(用 表示);
表示);(3)若关于
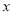 不等式
不等式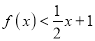 的解集中恰好有两个整数解,求
的解集中恰好有两个整数解,求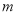 的取值范围.
的取值范围.
相关试题

