【题目】已知关于x的函数y= ![]() (t∈R)的定义域为D,存在区间[a,b]D,f(x)的值域也是[a,b].当t变化时,b﹣a的最大值= .
(t∈R)的定义域为D,存在区间[a,b]D,f(x)的值域也是[a,b].当t变化时,b﹣a的最大值= .
参考答案:
【答案】![]()
【解析】解:关于x的函数y=f(x)= ![]() =(1﹣t)﹣
=(1﹣t)﹣ ![]() 的定义域为(﹣∞,0)∪(0,+∞),
的定义域为(﹣∞,0)∪(0,+∞),
且函数在(﹣∞,0)、(0,+∞)上都是增函数.
故有a=f(a),且b=f(b),即 a= ![]() ,b=
,b= ![]() .
.
即 a2+(t﹣1)a+t2=0,且 b2+(t﹣1)b+t2=0,
故a、b是方程x2+(t﹣1)x+t2=0的两个同号的实数根.
由判别式大于0,容易求得t∈(﹣1, ![]() ).
).
而当t=0时,函数为y=1,不满足条件,故t∈(﹣1, ![]() )且t≠0.
)且t≠0.
由韦达定理可得b﹣a= ![]() =
= ![]() ,故当t=﹣
,故当t=﹣ ![]() 时,b﹣a取得最大值为
时,b﹣a取得最大值为 ![]() ,
,
故答案为: ![]() .
.
由函数的单调性可得a=f(a),且b=f(b),故a、b是方程x2+(t﹣1)x+t2=0的两个同号的实数根.由判别式大于0,容易求得t∈(﹣1, ![]() ).由韦达定理可得b﹣a=
).由韦达定理可得b﹣a= ![]() =
= ![]() ,利用二次函数的性质求得b﹣a的最大值.
,利用二次函数的性质求得b﹣a的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)在其定义域的一个子集[a,b]上存在实数 (a<m<b),使f(x)在m处的导数f′(m)满足f(b)﹣f(a)=f′(m)(b﹣a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数f(x)=
 x3﹣x2在[0,b]上恰有两个“中值点”,则实数b的取值范围是 .
x3﹣x2在[0,b]上恰有两个“中值点”,则实数b的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2},
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
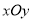 中,已知圆
中,已知圆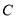 :
: 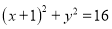 ,点
,点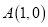 ,点
,点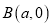 (
(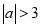 ),以
),以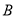 为圆心,
为圆心, 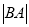 为半径作圆,交圆
为半径作圆,交圆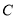 于点
于点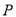 ,且
,且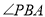 的平分线交线段
的平分线交线段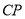 于点
于点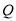 .
.
(1)当
 变化时,点
变化时,点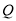 始终在某圆锥曲线
始终在某圆锥曲线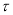 上运动,求曲线
上运动,求曲线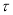 的方程;
的方程;(2)已知直线
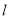 过点
过点 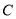 ,且与曲线
,且与曲线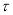 交于
交于 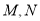 两点,记
两点,记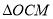 面积为
面积为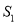 ,
, 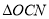 面积为
面积为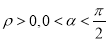 ,求
,求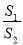 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 的离心率为
的离心率为 ,过左焦点
,过左焦点 且斜率为
且斜率为 的直线交椭圆
的直线交椭圆 于
于 ,
,  两点,线段
两点,线段 的中点为
的中点为 ,直线
,直线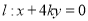 交椭圆
交椭圆 于
于 ,
,  两点.
两点.(I)求椭圆
 的方程.
的方程.(II)求证:点
 在直线
在直线 上.
上.(III)是否存在实数
 ,使得
,使得 的面积是
的面积是 面积的
面积的 倍?若存在,求出
倍?若存在,求出 的值.若不存在,说明理由.
的值.若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是空间两条直线,
是空间两条直线,  是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )A. 当
 时,“
时,“ ”是“
”是“ ”的充要条件
”的充要条件B. 当
 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. 当
 时,“
时,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件D. 当
 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围.
相关试题

