【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
(1)求椭圆C的标准方程;
(2)经过椭圆C右焦点的直线l和椭圆C交于A,B两点,点P在椭圆上,且 ![]() =2
=2 ![]() ,其中O为坐标原点,求直线l的斜率.
,其中O为坐标原点,求直线l的斜率.
参考答案:
【答案】
(1)解:由椭圆的离心率e= ![]() =
= ![]() ,a=
,a= ![]() c,
c,
由b2=a2﹣c2,则b=c,
设a=2λ,b=c= ![]() λ,λ>0,
λ,λ>0,
椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点,
∴M(c, ![]() ),代入椭圆中得:
),代入椭圆中得: ![]() +
+ ![]() =1,即
=1,即 ![]() +
+ ![]() =1,解得:λ=
=1,解得:λ= ![]() ,∴a=2
,∴a=2 ![]() ,b=c=2,
,b=c=2,
故椭圆方程为: ![]()
(2)解:设A(x1,y1),B(x2,y2),P(x0,y0),则 ![]() =(x1,y1),
=(x1,y1), ![]() =(x0﹣x2,y0﹣y2),
=(x0﹣x2,y0﹣y2),
由 ![]() =2
=2 ![]() ,
,
∴(x1,y1)=2(x0﹣x2,y0﹣y2)
∴ 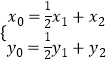 ,
,
由于A,B,P均在椭圆x2+2y2=8上,
∴ ![]() ①,
①, ![]() ②,
②, ![]() ③;
③;
由③可知: ![]() (
( ![]() )+(
)+( ![]() )+(x1x2+2y1y2)=8,
)+(x1x2+2y1y2)=8,
将第①②代入上式得:x1x2+2y1y2=﹣2,④
由直线l的斜率不为零,设直线l方为x=my+2,
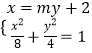 ,整理得:(m2+2)y2+4my﹣4=0,
,整理得:(m2+2)y2+4my﹣4=0,
由韦达定理y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
将④变形为:(my1+2)(my2+2)+2y1y2=﹣2,
即(m2+2)y1y2+2m(y1+y2)+6=0,
∴2﹣ ![]() =0,解得:m2=
=0,解得:m2= ![]() ,m=±
,m=± ![]() ,
,
∵直线的斜率k= ![]() =±
=± ![]() ,
,
故直线l的斜率为± ![]()
【解析】(1)由题意可知:e= ![]() 知,即a=
知,即a= ![]() c,则b=c,设a=2λ,b=c=
c,则b=c,设a=2λ,b=c= ![]() λ,λ>0,将M(c,
λ,λ>0,将M(c, ![]() ),代入,即可求得λ的值,求得椭圆C的标准方程;(2)由题意可知则
),代入,即可求得λ的值,求得椭圆C的标准方程;(2)由题意可知则 ![]() =(x1 , y1),
=(x1 , y1), ![]() =(x0﹣x2 , y0﹣y2),
=(x0﹣x2 , y0﹣y2), ![]() =2
=2 ![]() ,即(x1 , y1)=2(x0﹣x2 , y0﹣y2),由于A,B,P均在椭圆x2+2y2=8上,则
,即(x1 , y1)=2(x0﹣x2 , y0﹣y2),由于A,B,P均在椭圆x2+2y2=8上,则 ![]() ,整理可得:x1x2+2y1y2=﹣2,设直线l方为x=my+2,代入椭圆方程,由韦达定理可知代入可知:2﹣
,整理可得:x1x2+2y1y2=﹣2,设直线l方为x=my+2,代入椭圆方程,由韦达定理可知代入可知:2﹣ ![]() =0,解得m的值,直线l的斜率为
=0,解得m的值,直线l的斜率为 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,函数
,函数 .
.(1)求
 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;(2)若
 ,
,  ,求
,求 的值;
的值;(3)若函数
 在区间
在区间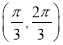 上是单调递增函数,求正数
上是单调递增函数,求正数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系
 的坐标平面
的坐标平面 内,若函数
内,若函数 的图象与
的图象与 轴围成一个封闭区域
轴围成一个封闭区域 ,将区域
,将区域 沿
沿 轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域 面积相等,则此圆柱的体积为__________.
面积相等,则此圆柱的体积为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[100,110),[110,120),[120,130)三组内的学生中,用分层抽样的方法选取28人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为
 ,各局比赛的结果都相互独立,第1局甲当裁判.
,各局比赛的结果都相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.
相关试题

