【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,函数
,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)0.
;(2)0.
【解析】
(1)由题意可得![]() ,由此求得a,b的值.
,由此求得a,b的值.
(2)利用整体换元法将![]() 化为二次型函数,分类讨论求得最大值,即可求得a值.
化为二次型函数,分类讨论求得最大值,即可求得a值.
(1)由题意![]() ,所以
,所以![]() 时,
时,![]() 最大,
最大,![]() 时,
时,![]() 最小,
最小,
可得![]() ,∴
,∴![]() ;
;
(2)∴g(x)=f(x)+cos2x
=1+asinx+cos2x
=2+asinx﹣sin2x
![]() 2﹣(sinx-
2﹣(sinx-![]() )2,
)2,
令t=sinx,
g(t)![]() 2﹣(t
2﹣(t![]() )2,∵t∈[
)2,∵t∈[![]() ,1],
,1],
分类讨论:
若![]() ,即a<-2,
,即a<-2,
gmax=g(![]() )
)![]() =2,故a
=2,故a![]() ;(舍去);
;(舍去);
若![]() 1即﹣2≤a≤2,
1即﹣2≤a≤2,
gmax=g(![]() )
)![]() 2=2,得a=0(舍去);
2=2,得a=0(舍去);
若![]() 1,即a>2,
1,即a>2,
gmax=g(1)![]() 2+a-1=2,得a=1(舍去)
2+a-1=2,得a=1(舍去)
∴可得:a=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  ,在
,在 处的切线方程为
处的切线方程为 .
.(1)求
 ,
,  ;
;(2)若
 ,证明:
,证明:  .
.【答案】(1)
 ,
, 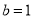 ;(2)见解析
;(2)见解析【解析】试题分析:(1)求出函数的导数,得到关于
 的方程组,解出即可;
的方程组,解出即可;(2)由(1)可知
 ,
,  ,
,由
 ,可得
,可得 ,令
,令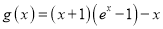 , 利用导数研究其单调性可得
, 利用导数研究其单调性可得 ,
,从而证明
 .
.试题解析:((1)由题意
 ,所以
,所以 ,
,又
 ,所以
,所以 ,
, 若
 ,则
,则 ,与
,与 矛盾,故
矛盾,故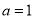 ,
,  .
.(2)由(1)可知
 ,
, 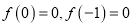 ,
,由
 ,可得
,可得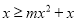 ,
,令
 ,
,  ,
,令

当
 时,
时,  ,
,  单调递减,且
单调递减,且 ;
;当
 时,
时,  ,
,  单调递增;且
单调递增;且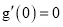 ,
,所以
 在
在 上当单调递减,在
上当单调递减,在 上单调递增,且
上单调递增,且 ,
,故
 ,
,故
 .
.【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
,  为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,若直线
,若直线 与曲线
与曲线 相切;
相切;(1)求曲线
 的极坐标方程;
的极坐标方程;(2)在曲线
 上取两点
上取两点 ,
,  与原点
与原点 构成
构成 ,且满足
,且满足 ,求面积
,求面积 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a,b,c分别是角A,B,C的对边,b=
 sinB,且满足tanA+tanC=
sinB,且满足tanA+tanC=  . (Ⅰ)求角C和边c的大小;
. (Ⅰ)求角C和边c的大小;
(Ⅱ)求△ABC面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图(1)将△AEF沿EF折起到△A1EF的位置,使二面角A1﹣EF﹣B成直二面角,连结A1B、A1P(如图(2)).

(1)求证:A1E⊥平面BEP;
(2)求二面角B﹣A1P﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 ,
, 是函数
是函数 (
( ,
,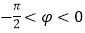 )图象上的任意两点,且角
)图象上的任意两点,且角 的终边经过点
的终边经过点 ,若
,若 时,
时,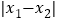 的最小值为
的最小值为 .
.(1)求函数
 的解析式;
的解析式;(2)当
 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 ﹣k(
﹣k(  +lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
+lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆
 +
+  =1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,  =2
=2  ,△DF1F2的面积为
,△DF1F2的面积为  . (Ⅰ)求该椭圆的标准方程;
. (Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.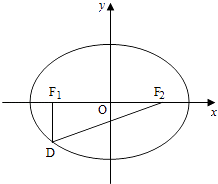
相关试题

