【题目】袋中装有大小形状完全相同的5个小球,其中3个白球的标号分别为1、 2 、3, 2 个黑球的标号分别为1、3.
(Ⅰ)从袋中随机摸出两个球,求摸到的两球颜色与标号都不相同的概率;
(Ⅱ)从袋中有放回地摸球,摸两次,每次摸出一个球,求摸出的两球的标号之和小于4 的概率.
参考答案:
【答案】(1) ![]() .
.
(2)![]() .
.
【解析】分析:(1)记5个球为白1、白2、白3、黑1、黑3,由此列举法能求出从中摸两个球,摸到的两球颜色与标号都不相同的概率.
(2)从中有放回的摸两次,每次摸球有5种结果,所以共有25种情况,利用列举法能求出摸出的两球的标号之和小于4的概率.
详解:
(Ⅰ)记5个球为白1、白2、白3、黑1、黑3,从中摸两个球共有:(白1、白2)、
(白1、白3)、(白1、黑1)、(白1、黑3)、(白2、白3)、(白2、黑1)、(白2、黑3)、(白3、黑1)、
(白3、黑3)、(黑1、黑3)共10种情况
两球颜色和标号都不相同的有:(白1、黑3)、(白2、黑1)、(白2、黑3)、(白3、黑1)
共 4 种情况,则所求概率为![]()
(Ⅱ)从中有放回的摸两次,每次摸球有5种结果,所以共有 25种情况
其中标号之和小于 4 的有(白1、白1)、(白1、黑1)、(黑1、白1)、(黑1、黑1)、(白
1、白2)、(黑1、白2)、(白2、白1)、(白2、黑1)共8种情况
所求概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】提高过江大桥的车辆通行的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度
 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,就会造成堵塞,此时车流速度为0;当
车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
 时,
时,车流速度
 是车流密度
是车流密度 的一次函数.
的一次函数.(1)当
 时,求函数
时,求函数 的表达式;
的表达式;(2)如果车流量(单位时间内通过桥上某观测点的车辆数)
 (单位:辆/小时),那么当车流密度
(单位:辆/小时),那么当车流密度 为多大时,车流量
为多大时,车流量 可以达到最大,并求出最大值.(精确到
可以达到最大,并求出最大值.(精确到 辆/小时).
辆/小时). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆柱形圆木的底面半径为1 m,长为10 m,将此圆木沿轴所在的平面剖成两部分.现要把其中一部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设
 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求
 的值,使体积V最大;
的值,使体积V最大;(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.

(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD-A1B1C1D1中,下列说法正确的是____ (填序号).
(1)直线AC1在平面CC1B1B内.
(2)设正方形ABCD与A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1.
(3)由A、C1、B1确定的平面是ADC1B1.
(4)由A、C1、B1确定的平面与由A、C1、D确定的平面是同一个平面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上的点,且AM=AN=1.
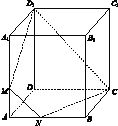
(1)证明:M,N,C,D1四点共面;
(2)平面MNCD1将此正方体分为两部分,求这两部分的体积之比.
相关试题

