【题目】已知函数f(x)=1+a( ![]() )x+(
)x+( ![]() )x .
)x .
(1)当a=﹣2,x∈[1,2]时,求函数f(x)的最大值与最小值;
(2)若函数f(x)在[1,+∞)上都有﹣2≤f(x)≤3,求实数a的取值范围.
参考答案:
【答案】
(1)解:令t=( ![]() )x,则y=f(x)=1+at+t2,
)x,则y=f(x)=1+at+t2,
当a=﹣2,x∈[1,2]时,y=f(x)=1﹣2t+t2,t∈[ ![]() ,
, ![]() ],
],
当t= ![]() ,即x=2时,函数f(x)的最大值为
,即x=2时,函数f(x)的最大值为 ![]() ,
,
当t= ![]() ,即x=1时,函数f(x)的最小值为
,即x=1时,函数f(x)的最小值为 ![]()
(2)解:若函数f(x)在[1,+∞)上都有﹣2≤f(x)≤3,
则y=1+at+t2,在(0, ![]() ]上都有﹣2≤y≤3,
]上都有﹣2≤y≤3,
由函数y=1+at+t2的图象是开口朝上,且以直线t= ![]() 为对称轴的直线,
为对称轴的直线,
故当 ![]() ≤0,即a≥0时,1+
≤0,即a≥0时,1+ ![]() a+
a+ ![]() ≤3,解得:a∈[0,
≤3,解得:a∈[0, ![]() ]
]
当0< ![]() <
< ![]() ,即
,即 ![]() <a<0时,
<a<0时,  ,解得:a∈(
,解得:a∈( ![]() ,0),
,0),
当 ![]() ≥
≥ ![]() ,即a≤
,即a≤ ![]() 时,1+
时,1+ ![]() a+
a+ ![]() ≥﹣2,解得:a∈[﹣
≥﹣2,解得:a∈[﹣ ![]() ,
, ![]() ]
]
综相可得a∈[﹣ ![]() ,
, ![]() ]
]
【解析】令t=( ![]() )x , 则y=f(x)=1+at+t2 , (1)当a=﹣2,x∈[1,2]时,y=f(x)=1﹣2t+t2 , t∈[
)x , 则y=f(x)=1+at+t2 , (1)当a=﹣2,x∈[1,2]时,y=f(x)=1﹣2t+t2 , t∈[ ![]() ,
, ![]() ],结合二次函数的图象和性质,可得函数f(x)的最大值与最小值;(2)若函数f(x)在[1,+∞)上都有﹣2≤f(x)≤3,y=1+at+t2 , 在(0,
],结合二次函数的图象和性质,可得函数f(x)的最大值与最小值;(2)若函数f(x)在[1,+∞)上都有﹣2≤f(x)≤3,y=1+at+t2 , 在(0, ![]() ]上都有﹣2≤y≤3,结合二次函数的图象和性质,可得实数a的取值范围.
]上都有﹣2≤y≤3,结合二次函数的图象和性质,可得实数a的取值范围.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校
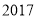 届高三文(1)班在一次数学测验中,全班
届高三文(1)班在一次数学测验中,全班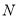 名学生的数学成绩的频率分布直方图如下,已知分数在
名学生的数学成绩的频率分布直方图如下,已知分数在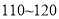 的学生数有
的学生数有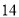 人.
人.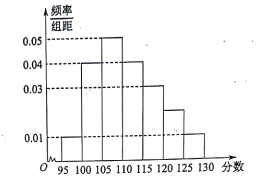
(1)求总人数
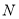 和分数在
和分数在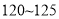 的人数
的人数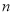 ;
;(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现在从比分数在
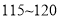 名学生(男女生比例为
名学生(男女生比例为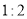 )中任选
)中任选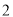 人,求其中至多含有
人,求其中至多含有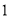 名男生的概率.
名男生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2(4x+1)﹣x,g(x)=log2a+log2(2x﹣
 )(a>0,x>1).
)(a>0,x>1).
(1)证明函数f(x)为偶函数;
(2)若函数f(x)﹣g(x)只有一个零点,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)当
 时,若对任意
时,若对任意 ,都有
,都有 成立,求
成立,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C所对的边分别为a,b,c,已知sinA+sinC=psinB且
 .若角B为锐角,则p的取值范围是( )
.若角B为锐角,则p的取值范围是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为吸引顾客,某公司在商场举办电子游戏活动.对于
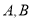 两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏
两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏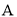 ,若绿灯闪亮,获得
,若绿灯闪亮,获得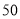 分,若绿灯不闪亮,则扣除
分,若绿灯不闪亮,则扣除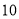 分(即获得
分(即获得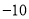 分),绿灯闪亮的概率为
分),绿灯闪亮的概率为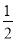 ;玩一次游戏
;玩一次游戏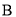 ,若出现音乐,获得
,若出现音乐,获得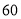 分,若没有出现音乐,则扣除
分,若没有出现音乐,则扣除 分(即获得
分(即获得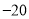 分),出现音乐的概率为
分),出现音乐的概率为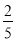 .玩多次游戏后累计积分达到
.玩多次游戏后累计积分达到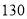 分可以兑换奖品.
分可以兑换奖品.(1)记
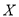 为玩游戏
为玩游戏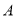 和
和 各一次所得的总分,求随机变量
各一次所得的总分,求随机变量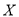 的分布列和数学期望;
的分布列和数学期望;(2)记某人玩
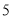 次游戏
次游戏 ,求该人能兑换奖品的概率.
,求该人能兑换奖品的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
相关试题

