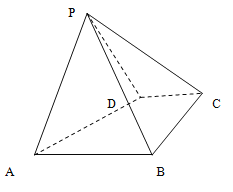
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: (Ⅰ)取![]() 的中
的中![]() ,连接
,连接![]() ,由三角形
,由三角形![]() 是等腰三角形,则
是等腰三角形,则![]() ,又
,又![]() ,可得
,可得![]() ,从而证出
,从而证出![]() ,可得
,可得![]() ; (Ⅱ)取
; (Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,可证明四边形
,可证明四边形![]() 为平行四边形,进一步证明
为平行四边形,进一步证明![]() ,可得三角形
,可得三角形![]() 是直角三角形,由三角形面积公式可得面积.
是直角三角形,由三角形面积公式可得面积.
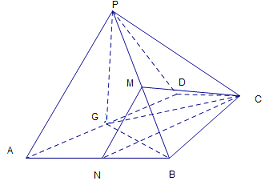
试题解析:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() 且
且![]() ,
,
∴![]() 是正三角形,且
是正三角形,且![]() ,
,
又∵![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,且
,且![]() 平面
平面![]()
∴![]()
(Ⅱ)解:存在,理由如下:
分别取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ;
;
∵![]() 是梯形,
是梯形,![]() 且
且![]() ,
,
∴![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
∴![]()
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,
,![]()
∴平面![]() 平面
平面![]()
∵侧面![]() ,且平面
,且平面![]() 平面
平面![]()
由(Ⅰ)知,![]() 平面
平面![]() ,若四棱锥
,若四棱锥![]() 的体积等于
的体积等于![]() ,
,
则![]() ,所以
,所以![]()
在![]() 和
和![]() 中,
中,![]()
∴![]() ,则
,则![]()
∴![]() 是直角三角形,则
是直角三角形,则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是(-∞,+∞)上的奇函数,且f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于( )
A. 0.5 B. -0.5
C. 1.5 D. -1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=loga(x+3)-1(a>0,a≠1)的图象恒过定点A.
(1) 求点A的坐标;
(2) 若点A在直线mx+ny+1=0上,其中m,n都是正数,求
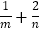 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 若x>1,求x+
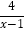 的最小值;
的最小值;(2) 若x>0,y>0,且2x+8y-xy=0,求xy的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度
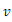 (单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当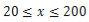 时,车流速度
时,车流速度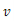 是车流密度x的一次函数.
是车流密度x的一次函数.①当
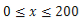 时,求函数
时,求函数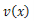 的表达式.
的表达式.②当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
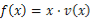 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
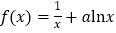 ,
,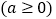 .
.(Ⅰ)若
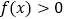 恒成立,求
恒成立,求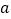 的取值范围;
的取值范围;(Ⅱ)设
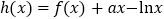 ,
,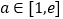 ,(
,(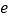 为自然对数的底数).是否存在常数
为自然对数的底数).是否存在常数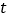 ,使
,使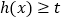 恒成立,若存在,求出
恒成立,若存在,求出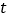 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
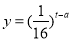 (a为常数),如图所示.根据图中提供的信息,回答下列问题:
(a为常数),如图所示.根据图中提供的信息,回答下列问题:
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为_________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过_________小时后,学生才能回到教室.
相关试题

