【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

参考答案:
【答案】![]()
【解析】如下图,连接DO交BC于点G,设D,E,F重合于S点,正三角形的边长为x(x>0),则![]()
![]() .
.
![]()
![]() ,
,

 ,
,
![]() 三棱锥的体积
三棱锥的体积
![]() .
.
设![]() ,x>0,则
,x>0,则![]() ,
,
令![]() ,即
,即![]() ,得
,得![]() ,易知
,易知![]() 在
在![]() 处取得最大值.
处取得最大值.
∴![]() .
.

点睛:对于三棱锥最值问题,需要用到函数思想进行解决,本题解决的关键是设好未知量,利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决,当变量是高次时需要用到求导的方式进行解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥S﹣ABC中,AB⊥BC,AB=BC=
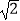 ,SA=SC=2,二面角S﹣AC﹣B的余弦值是
,SA=SC=2,二面角S﹣AC﹣B的余弦值是 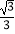 ,若S、A、B、C都在同一球面上,则该球的表面积是 .
,若S、A、B、C都在同一球面上,则该球的表面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2﹣bx+c≥0的解集为{x|1≤x≤2},则cx2+bx+a≤0的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为

(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC=2,原点O是BC的中点,点A的坐标为 (
 ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°. 
(1)求向量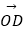 的坐标
的坐标
(2)求向量 的夹角的余弦值大小.
的夹角的余弦值大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
(Ⅰ)在所给图中画出平面ABD1与平面B1EC的交线(不必说明理由);
(Ⅱ)证明:BD1∥平面B1EC;
(Ⅲ)求平面ABD1与平面B1EC所成锐二面角的大小.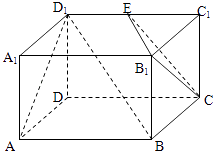
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:y=cos x,C2:y=sin (2x+
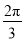 ),则下面结论正确的是
),则下面结论正确的是A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
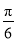 个单位长度,得到曲线C2
个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
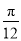 个单位长度,得到曲线C2
个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的
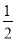 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移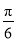 个单位长度,得到曲线C2
个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的
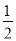 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移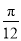 个单位长度,得到曲线C2
个单位长度,得到曲线C2
相关试题

