【题目】在三棱锥S﹣ABC中,AB⊥BC,AB=BC= ![]() ,SA=SC=2,二面角S﹣AC﹣B的余弦值是
,SA=SC=2,二面角S﹣AC﹣B的余弦值是 ![]() ,若S、A、B、C都在同一球面上,则该球的表面积是 .
,若S、A、B、C都在同一球面上,则该球的表面积是 .
参考答案:
【答案】6π
【解析】解:如图所示:
取AC中点D,连接SD,BD,则由AB=BC,SA=SC得出SD⊥AC,BD⊥AC,
∴∠SDB为S﹣AC﹣B的平面角,且AC⊥面SBD.
由题意:AB⊥BC,AB=BC= ![]() ,易得:△ABC为等腰直角三角形,且AC=2,
,易得:△ABC为等腰直角三角形,且AC=2,
又∵BD⊥AC,故BD=AD= ![]() AC,
AC,
在△SBD中,BD= ![]() =
= ![]() =1,
=1,
在△SAC中,SD2=SA2﹣AD2=22﹣12=3,
在△SBD中,由余弦定理得SB2=SD2+BD2﹣2SDBDcos∠SDB=3+1﹣2× ![]() =2,
=2,
满足SB2=SD2﹣BD2 , ∴∠SBD=90°,SB⊥BD,
又SB⊥AC,BD∩AC=D,∴SB⊥面ABC.
以SB,BA,BC为顶点可以补成一个棱长为 ![]() 的正方体,S、A、B、C都在正方体的外接球上,
的正方体,S、A、B、C都在正方体的外接球上,
正方体的对角线为球的一条直径,所以2R= ![]() ,R=
,R= ![]() ,球的表面积S=4
,球的表面积S=4 ![]() =6π.
=6π.
所以答案是:6π.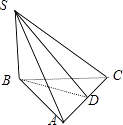
【考点精析】本题主要考查了球内接多面体的相关知识点,需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4—5:不等式选讲]
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把函数f(x)=sin(2x+φ)(|φ|<
 )的图象上的所有点向左平移
)的图象上的所有点向左平移 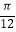 个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
A.y=g(x)在(0, )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x=  对称
对称
B.y=g(x)在(0, )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x=  对称
对称
C.y=g(x)在(0, )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x=  对称
对称
D.y=g(x)在(0, )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x=  对称
对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ae2x+(a﹣2) ex﹣x.
ae2x+(a﹣2) ex﹣x.(1)讨论
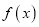 的单调性;
的单调性;(2)若
 有两个零点,求a的取值范围.
有两个零点,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2﹣bx+c≥0的解集为{x|1≤x≤2},则cx2+bx+a≤0的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为

(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

相关试题

