【题目】下列五个命题中:
①函数y=loga(2x﹣1)+2015(a>0且a≠1)的图象过定点(1,2015);
②若定义域为R函数f(x)满足:对任意互不相等的x1、x2都有(x1﹣x2)[f(x1)﹣f(x2)]>0,则f(x)是减函数;
③f(x+1)=x2﹣1,则f(x)=x2﹣2x;
④若函数f(x)=![]() 是奇函数,则实数a=﹣1;
是奇函数,则实数a=﹣1;
⑤若a=![]() (c>0,c≠1),则实数a=3.
(c>0,c≠1),则实数a=3.
其中正确的命题是 .(填上相应的序号).
参考答案:
【答案】①③⑤
【解析】解:对于①,函数y=f(x)=loga(2x﹣1)+2015(a>0且a≠1),有f(1)=2015,即其图象过定点(1,2015),故①正确;
对于②,若定义域为R函数f(x)满足:对任意互不相等的x1、x2都有(x1﹣x2)[f(x1)﹣f(x2)]>0,即k= >0,则f(x)是增函数,故②错误;
>0,则f(x)是增函数,故②错误;
对于③,f(x+1)=x2﹣1=[(x+1)﹣1]2﹣1=(x+1)2﹣2(x+1),则f(x)=x2﹣2x,故③正确;
对于④,若函数f(x)=![]() 是奇函数,又其定义域为R,故f(0)=
是奇函数,又其定义域为R,故f(0)=![]() =0,解得实数a=1,故④错误;
=0,解得实数a=1,故④错误;
对于⑤,若a=![]() =log28(c>0,c≠1),则实数a=3,故⑤正确.
=log28(c>0,c≠1),则实数a=3,故⑤正确.
综上所述,正确选项为:①③⑤.
所以答案是:①③⑤.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间计划每天生产卡车模型、赛车模型、小汽车模型这三种玩具共100个,已知生产一个卡车模型需5分钟,生产一个赛车模型需7分钟,生产一个小汽车模型需4分钟,且生产一个卡车模型可获利润8元,生产一个赛车模型可获利润9元,生产一个小汽车模型可获利润6元.若总生产时间不超过10小时,该公司合理分配生产任务使每天的利润最大,则最大利润是______________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差大于零的等差数列
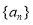 的前
的前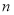 项和为
项和为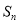 ,且
,且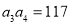 ,
,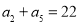 .
.(1)求数列
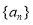 的通项公式;
的通项公式;(2)若数列
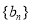 是等差数列,且
是等差数列,且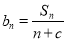 ,求非零常数
,求非零常数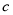 的值.
的值.(3)设
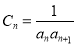 ,
,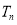 为数列
为数列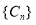 的前
的前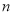 项和,是否存在正整数
项和,是否存在正整数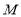 ,使得
,使得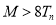 对任意的
对任意的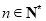 均成立?若存在,求出
均成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
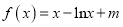 若曲线
若曲线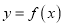 在
在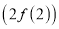 处的切线方程为
处的切线方程为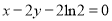 .
.(Ⅰ)求
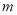 的值;
的值;(Ⅱ)若对于任意
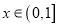 ,总有
,总有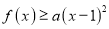 ,求实数
,求实数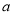 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=
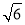 ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.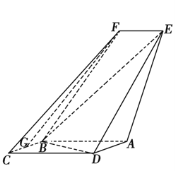
(1)求证:FG
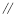 平面BED;
平面BED;(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
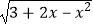 的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
(1)求A和f(x)的值域C;
(2)若A∩B=[2,3],求实数m的值;
(3)若CRB,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
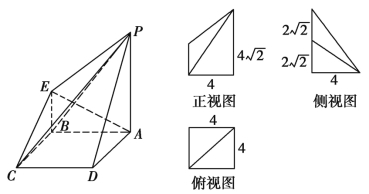
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
相关试题

