【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
, ![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,且
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,且![]() .设
.设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
参考答案:
【答案】(1)(2)
【解析】试题分析: 根据题意表示出所需的线段长度,再分别求三角形和扇形面积,从而表示出总面积,再根据题意要求求出函数的定义域;根据题意表示出“透光比”函数![]() ,借助求导,研究函数单调性求出最大值.
,借助求导,研究函数单调性求出最大值.
试题解析:(1)过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
所以![]() ,
,
![]() .
.
所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以定义域为
,所以定义域为![]() .
.
(2)矩形窗面的面积为![]() .
.
则透光区域与矩形窗面的面积比值为![]() .…10分
.…10分
设![]() ,
, ![]() .
.
则![]()
 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() ,
,
所以函数![]() 在
在![]() 上单调减.
上单调减.
所以当![]() 时,
时, ![]() 有最大值
有最大值![]() ,此时
,此时![]() (m).
(m).
答:(1)![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() ,定义域为
,定义域为![]() ;
;
(2)透光区域与矩形窗面的面积比值最大时, ![]() 的长度为1m.
的长度为1m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市有大型超市200家、中型超市400家、小型超市1400 家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A.70家
B.50家
C.20家
D.10家 -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}的前n项和为Sn , 已知a3=24,S11=0.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)当n为何值时,Sn最大,并求Sn的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)当
 时,求函数
时,求函数 的单调增区间;
的单调增区间;(2)设函数
 ,
,  .若函数
.若函数 的最小值是
的最小值是 ,求
,求 的值;
的值;(3)若函数
 ,
,  的定义域都是
的定义域都是 ,对于函数
,对于函数 的图象上的任意一点
的图象上的任意一点 ,在函数
,在函数 的图象上都存在一点
的图象上都存在一点 ,使得
,使得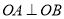 ,其中
,其中 是自然对数的底数,
是自然对数的底数,  为坐标原点.求
为坐标原点.求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个无穷数列
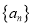 和
和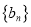 的前
的前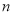 项和分别为
项和分别为 ,
, 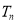 ,
,  ,
, 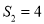 ,对任意的
,对任意的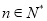 ,都有
,都有 .
.(1)求数列
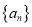 的通项公式;
的通项公式;(2)若
 为等差数列,对任意的
为等差数列,对任意的 ,都有
,都有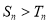 .证明:
.证明: 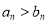 ;
;(3)若
 为等比数列,
为等比数列,  ,
, 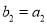 ,求满足
,求满足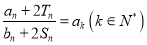
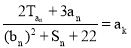 的
的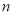 值.
值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
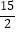 ,求AB的长.
,求AB的长. 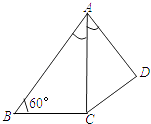
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是计算1+
 +
+ 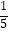 +…+
+…+  的值的一个程序框图,其中判断框内应填的是( )
的值的一个程序框图,其中判断框内应填的是( ) 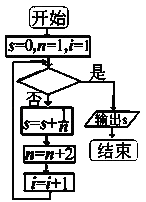
A.i>10
B.i<10
C.i>20
D.i<20
相关试题

