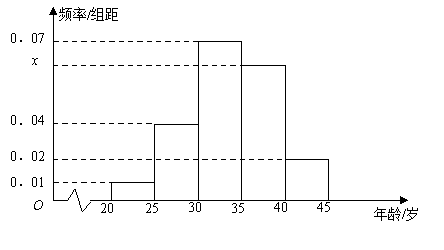
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者. 从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是: ![]() .
.
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人. 记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)由频率分布直方图中小长方形面积为对应概率,可得![]() ,即得
,即得![]() 的值,由总数与概率的乘积等于频数得年龄在
的值,由总数与概率的乘积等于频数得年龄在![]() 岁的人数为
岁的人数为![]() (Ⅱ)先按分层抽样得年龄“低于35岁”的人有6名,从而确定随机变量取法为0,1,2,3,再利用组合数求出对应概率,列表可得概率分布,最后根据数学期望公式求数学期望
(Ⅱ)先按分层抽样得年龄“低于35岁”的人有6名,从而确定随机变量取法为0,1,2,3,再利用组合数求出对应概率,列表可得概率分布,最后根据数学期望公式求数学期望
试题解析:(Ⅰ)∵小矩形的面积等于频率,∴除![]() 外的频率和为0.70,
外的频率和为0.70,
![]()
500名志愿者中,年龄在![]() 岁的人数为
岁的人数为![]() (人).
(人).
(Ⅱ)用分层抽样的方法,从中选取10名,则其中年龄“低于35岁”的人有6名,
“年龄不低于35岁”的人有4名. 故![]() 的可能取值为0,1,2,3,
的可能取值为0,1,2,3,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
故![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个球的体积之比为8:27,那么这两个球的表面积之比为( )
A. 2:3 B. 4:9 C. 8:27 D. 16:81
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
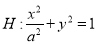 (
(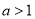 ),原点
),原点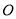 到直线
到直线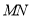 的距离为
的距离为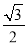 ,其中:点
,其中:点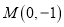 ,点
,点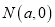 .
.(1)求该椭圆
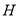 的离心率
的离心率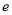 ;
;(2)经过椭圆右焦点
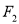 的直线
的直线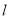 和该椭圆交于
和该椭圆交于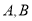 两点,点
两点,点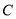 在椭圆上,
在椭圆上, 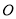 为原点,若
为原点,若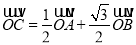 ,求直线
,求直线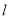 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 
 平面
平面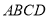 ,
,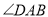 为直角,
为直角,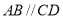 ,
, ,
,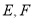 分别为
分别为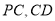 的中点.
的中点.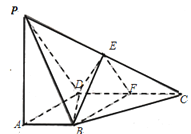
(Ⅰ)证明:
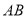
 平面
平面 ;
;(Ⅱ)若
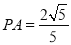 ,求二面角
,求二面角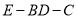 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,函数
,函数 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.(Ⅰ)求实数
 的值;
的值;(Ⅱ)若函数
 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;(Ⅲ)设
 是函数
是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,第二步归纳假设应写成( )
A.假设n=2k+1(k∈N*)正确,再推n=2k+3正确
B.假设n=2k﹣1(k∈N*)正确,再推n=2k+1正确
C.假设n=k(k∈N*)正确,再推n=k+1正确
D.假设n=k(k≥1)正确,再推n=k+2正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的一点与平面外的一点的连线与这个平面内的直线的关系是: .
相关试题

