搜索
【题目】（本小题满分10分）
已知如下等式： 
， 
， 
，
当
时，试猜想
的值，并用数学归纳法给予证明．
参考答案：
【答案】解：由已知，猜想
……………………………（2分）
下面用数学归纳法给予证明：
（1）当
时，由已知得原式成立； ………………………………………………（3分）
（2）假设当
时，原式成立，即
……（4分）
那么，当
时， 
=
故
时，原式也成立。……………………………………………………（11分）
由（1）、（2）知
成立 ……………（12分）
【解析】先猜想，然后再用数学归纳法进行证明.
证明时分两个步骤：第一步，先验证是当n=1时，等式是否成立；
第二步，假设n=k时，等式成立；再证明当n=k+1时，等式也成立，再证明时一定要用上归纳假设.否则证明无效
-
科目： 来源： 题型：
查看答案和解析>>【题目】为得到函数y=sin（2x+
）的图象，只需将函数y=sin2x的图象（ ）
A.向右平移 长度单位
B.向左平移 个长度单位
C.向右平移个
长度单位
D.向左平移 长度单位 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，圆C：x2+y2﹣8y+12=0，直线l：ax+y+2a=0．
（1）当a为何值时，直线l与圆C相切；
（2）当直线l与圆C相交于A、B两点，且AB=2
时，求直线l的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】随着社会发展，淮北市在一天的上下班时段也出现了堵车严重的现象。交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为T，其范围为[0，10]，分别有5个级别：T∈[0，2)畅通；T∈[2，4)基本畅通；T∈[4，6)轻度拥堵；T∈[6，8)中度拥堵；T∈[8，10]严重拥堵．早高峰时段(T≥3 )，从淮北市交通指挥中心随机选取了一至四马路之间50个交通路段，依据交通指数数据绘制的直方图如图所示：
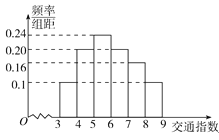
(I)据此直方图估算交通指数T∈[4，8)时的中位数和平均数；
(II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少？
(III)某人上班路上所用时间若畅通时为20分钟，基本畅通为30分钟，轻度拥堵为35分钟，中度拥堵为45分钟，严重拥堵为60分钟，求此人用时间的数学期望．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
.（I）讨论函数的单调性,并证明当
时，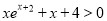 
;（Ⅱ）证明：当
时，函数
有最小值，设
最小值为
，求函数
的值域. -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两家商场对同一种商品开展促销活动，对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘，当指针指向阴影部分(图中两个阴影部分均为扇形，且每个扇形圆心角均为
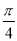，边界忽略不计)即为中奖·乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同)，它是红球的概率是
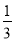，若从盒子中一次性摸出2球，且摸到的是2个相同颜色的球，即为中奖.
（Ⅰ）求实数
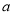的值；（Ⅱ）试问：购买该商品的顾客在哪家商场中奖的可能性大？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜
）的部分图象如图所示． 
（1）求函数f（x）的解析式；
（2）求函数g（x）=f（x﹣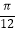
）﹣f（x+ 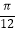）的单调递增区间．
相关试题
