第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
1. 学校有一条 30 米长的道路,计划在路的一旁栽树,每隔 3 米栽一棵。
(1) 如果只有一端栽树,共需要栽(
(2) 如果两端都不栽,共需要栽(
(3) 如果两端各栽一棵树,共需要栽(
(1) 如果只有一端栽树,共需要栽(
10
)棵;(2) 如果两端都不栽,共需要栽(
9
)棵;(3) 如果两端各栽一棵树,共需要栽(
11
)棵。
答案:
1.(1)10 (2)9 (3)11
2. 一个三角形的面积是 24 平方分米,这个三角形的底和高分别是多少分米?试列表看一看可能有几种情况。(要求底和高均为整数)

|底/分米|1|2|3|4|6|8|12|24|
|----|----|----|----|----|----|----|----|----|
|高/分米|48|24|16|12|8|6|4|2|
解题步骤:
1. 三角形面积公式:$ S = \frac{1}{2} × 底 × 高 $,已知$ S = 24 $平方分米,可得$ 底 × 高 = 48 $。
2. 找出48的所有正整数因数对:
$ (1, 48), (2, 24), (3, 16), (4, 12), (6, 8), (8, 6), (12, 4), (24, 2) $。
3. 因底和高为整数,且通常底和高顺序可互换,但题目未限定顺序,故列出所有可能情况如上表。
结论:共有8种情况。

|底/分米|1|2|3|4|6|8|12|24|
|----|----|----|----|----|----|----|----|----|
|高/分米|48|24|16|12|8|6|4|2|
解题步骤:
1. 三角形面积公式:$ S = \frac{1}{2} × 底 × 高 $,已知$ S = 24 $平方分米,可得$ 底 × 高 = 48 $。
2. 找出48的所有正整数因数对:
$ (1, 48), (2, 24), (3, 16), (4, 12), (6, 8), (8, 6), (12, 4), (24, 2) $。
3. 因底和高为整数,且通常底和高顺序可互换,但题目未限定顺序,故列出所有可能情况如上表。
结论:共有8种情况。
答案:
|底/分米|1|2|3|4|6|8|12|24|
|----|----|----|----|----|----|----|----|----|
|高/分米|48|24|16|12|8|6|4|2|
解题步骤:
1. 三角形面积公式:$ S = \frac{1}{2} × 底 × 高 $,已知$ S = 24 $平方分米,可得$ 底 × 高 = 48 $。
2. 找出48的所有正整数因数对:
$ (1, 48), (2, 24), (3, 16), (4, 12), (6, 8), (8, 6), (12, 4), (24, 2) $。
3. 因底和高为整数,且通常底和高顺序可互换,但题目未限定顺序,故列出所有可能情况如上表。
结论:共有8种情况。
|----|----|----|----|----|----|----|----|----|
|高/分米|48|24|16|12|8|6|4|2|
解题步骤:
1. 三角形面积公式:$ S = \frac{1}{2} × 底 × 高 $,已知$ S = 24 $平方分米,可得$ 底 × 高 = 48 $。
2. 找出48的所有正整数因数对:
$ (1, 48), (2, 24), (3, 16), (4, 12), (6, 8), (8, 6), (12, 4), (24, 2) $。
3. 因底和高为整数,且通常底和高顺序可互换,但题目未限定顺序,故列出所有可能情况如上表。
结论:共有8种情况。
3. 小王、小李、小英和小刚四人进行象棋比赛,如果每两人之间都进行一次比赛的话,他们之间一共要进行多少次比赛?请你用连线的方法解决。
答案:
3. 6次
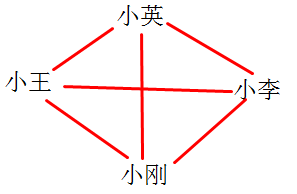
3. 6次

4. 明明到食堂里去买饭菜,食堂里共有 2 种素菜、2 种荤菜、1 种汤,他要各买 1 种,共有多少种不同的买法?
答案:
4. 4种
5. 用 2,3,4,5 可以组成多少个大于 3000 的四位数?
答案:
5. 18个
查看更多完整答案,请扫码查看


