《2025年导学练暑假作业五年级数学》

一、判断题。对的打“√”，错的打“×”。
1. 8 的倍数只有 16、24、32、40 这 4 个。 (×)
2. 给任何一个偶数加 1，得到的数一定是奇数。 (√)
3. 三个连续奇数的和是 21，这三个连续的奇数是 6、7、8。 (×)

答案： 1. × 2. √ 3. ×

1. 用阴影部分表示下面的分数，你发现了什么？

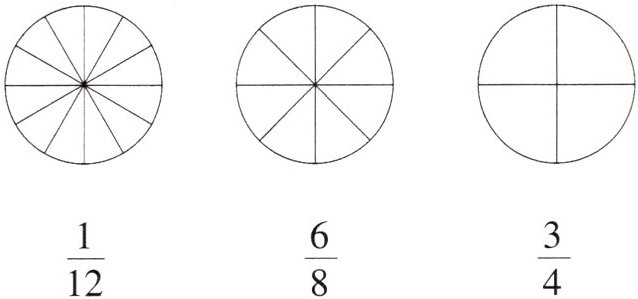
答案：
如图所示：

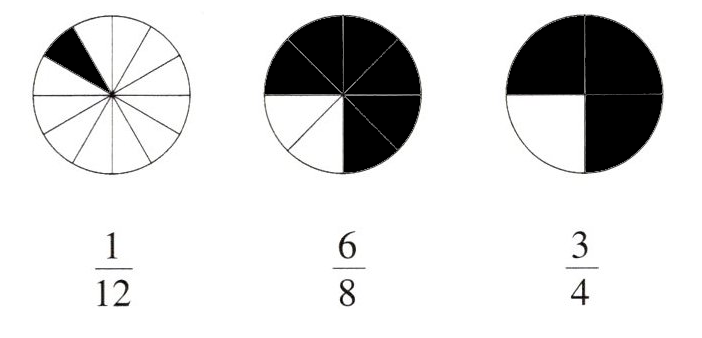
发现分数的分子和分母同时乘或除以一个相同的数（$0$除外），分数的大小不变。

2. 下面哪些情况看到的图形是？请在括号里打“√”。


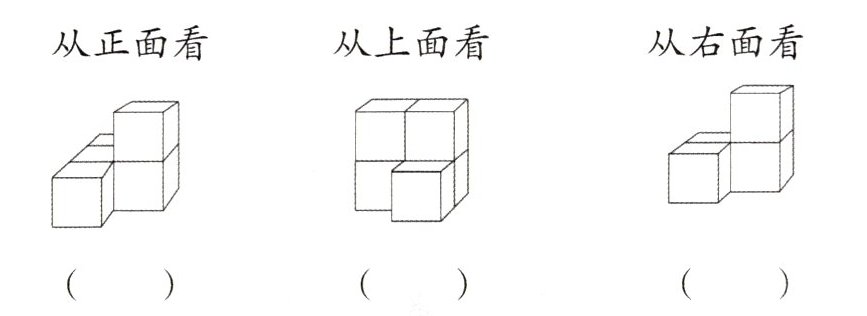
从正面看（√） 从右面看（√）

答案： 从正面看（ √） 从右面看（√ ）

三、用简便方法计算。
$\frac{3}{4}+99\frac{3}{4}+999\frac{3}{4}+9999\frac{3}{4}$
$\frac{1}{2000}+\frac{2}{2000}+\frac{3}{2000}+...+\frac{999}{2000}$

答案： 【解析】：
1. 计算$\frac{3}{4}+99\frac{3}{4}+999\frac{3}{4}+9999\frac{3}{4}$：
把$\frac{3}{4}$拆分成$4$个$\frac{1}{4}$相加，即$\frac{3}{4}=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$。
原式$=\left(99 + \frac{1}{4}+\frac{1}{4}\right)+\left(999+\frac{1}{4}+\frac{1}{4}\right)+\left(9999+\frac{1}{4}+\frac{1}{4}\right)+\frac{1}{4}$
$=(99 + \frac{1}{4})+(999+\frac{1}{4})+(9999+\frac{1}{4})+(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4})$
$=(99 + \frac{1}{4})+(999+\frac{1}{4})+(9999+\frac{1}{4}) + 1$
$=(100 - 1+\frac{1}{4})+(1000 - 1+\frac{1}{4})+(10000 - 1+\frac{1}{4})+1$
$=(100+1000 + 10000)+(\frac{1}{4}+\frac{1}{4}+\frac{1}{4})-(1 + 1+1)+1$
$=11100+\frac{3}{4}-3 + 1$
$=11100+\frac{3}{4}-2$
$=11098+\frac{3}{4}=11098\frac{3}{4}$。
2. 计算$\frac{1}{2000}+\frac{2}{2000}+\frac{3}{2000}+\cdots+\frac{999}{2000}$：
根据同分母分数加法法则，$\frac{1}{2000}+\frac{2}{2000}+\frac{3}{2000}+\cdots+\frac{999}{2000}=\frac{1 + 2+3+\cdots+999}{2000}$。
由等差数列求和公式$S_n=\frac{n(a_1 + a_n)}{2}$（其中$n$是项数，$a_1$是首项，$a_n$是末项），这里$n = 999$，$a_1=1$，$a_n = 999$。
则$1 + 2+3+\cdots+999=\frac{999\times(1 + 999)}{2}=\frac{999\times1000}{2}=999\times500$。
所以$\frac{1 + 2+3+\cdots+999}{2000}=\frac{999\times500}{2000}=\frac{999}{4}=249.75$。
【答案】：$11098\frac{3}{4}$；$249.75$