《2025年暑假作业假期园地八年级合订本中原农民出版社》

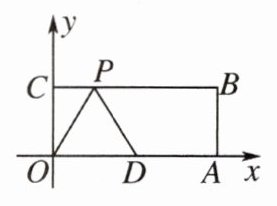
11. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为$(10,0),(0,4)$,点D是OA的中点,点P在BC边上运动.当$△ODP$是腰长为5的等腰三角形时,求点P的坐标.

$(2,4)$或$(3,4)$或$(8,4)$

答案： 【解析】：
已知点$A(10,0)$，点$D$是$OA$的中点，则$OD=\frac{1}{2}OA = 5$。
因为$\triangle ODP$是腰长为$5$的等腰三角形，所以分三种情况讨论：
1. 当$OD = OP = 5$时：
在$Rt\triangle OCP$中，$OC = 4$，$OP = 5$，根据勾股定理$CP=\sqrt{OP^{2}-OC^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=\sqrt{9}=3$，此时点$P$的坐标为$(3,4)$。
2. 当$OD = DP = 5$时：
过点$D$作$DE\perp BC$于点$E$，则$DE = OC = 4$，$OE = AD = 5$。
在$Rt\triangle DEP$中，$DP = 5$，$DE = 4$，根据勾股定理$EP=\sqrt{DP^{2}-DE^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25 - 16}=\sqrt{9}=3$。
当点$P$在点$E$左侧时，$CP = 5 - 3 = 2$，此时点$P$的坐标为$(2,4)$。
当点$P$在点$E$右侧时，$CP = 5 + 3 = 8$，此时点$P$的坐标为$(8,4)$。
【答案】：$(2,4)$或$(3,4)$或$(8,4)$

12. 如图所示,A城气象台测得台风中心在A城正西方向320 km的B处,以每小时40 km的速度向北偏东$60^{\circ }$的BF方向移动,距离台风中心200 km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?A城受到这次台风的影响
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?6小时(提示:在直角三角形中,$30^{\circ }$的锐角对的直角边等于斜边的一半)

答案： 【解析】：
### $(1)$判断$A$城是否受到这次台风的影响
过$A$作$AC\perp BF$于$C$。
在$Rt\triangle ABC$中，$\angle CBA = 30^{\circ}$，$AB = 320km$。
根据在直角三角形中，$30^{\circ}$的锐角对的直角边等于斜边的一半，可得$AC=\frac{1}{2}AB$。
所以$AC=\frac{1}{2}\times320 = 160(km)$。
因为$160\lt200$，即$A$城到台风中心移动路线的距离小于受台风影响的范围半径，所以$A$城受到这次台风的影响。
### $(2)$计算$A$城遭受这次台风影响的时间
设台风中心移动到$D$点时$A$城开始受影响，移动到$E$点时$A$城结束受影响，则$AD = AE = 200km$。
在$Rt\triangle ACD$中，根据勾股定理$CD=\sqrt{AD^{2}-AC^{2}}$。
已知$AD = 200km$，$AC = 160km$，则$CD=\sqrt{200^{2}-160^{2}}=\sqrt{(200 + 160)(200 - 160)}=\sqrt{360\times40}=\sqrt{14400}=120(km)$。
同理，在$Rt\triangle ACE$中，$CE = CD = 120km$，所以$DE=CD + CE=240km$。
已知台风速度是每小时$40km$，根据时间$t=\frac{s}{v}$（$s$是路程，$v$是速度），可得$A$城遭受台风影响的时间$t=\frac{240}{40}=6$（小时）。
【答案】：
$(1)$ $A$城受到这次台风的影响。
$(2)$ $A$城遭受这次台风影响的时间为$6$小时。